Dynamics of single-cell division and death in the presence of antibiotics
[2023: Explanations still to be write]
Viafx24
Pr. [2023: protected identity] has proof-readed this manuscript and has significantly improved it. Moreover, some paragraphs may have been directly written by him (I don’t precisely remember). In that case, the corresponding “paternity” of those paragraphs should be attributed to him.
Summary
An important example of phenotypic diversity is the phenomenon of bacterial persistence: a subpopulation of cells is resistant to an antibiotic but this trait is not inherited by the progeny. Observations in Escherichia coli suggested that persistent cells are in a reversible non-dividing state, resulting in the assumption that the bactericidal efficacy of an antibiotic is directly proportional to the growth rate. By performing experiments at the single-cell level using a microfluidic-microscopy system, the team of Prof. [2023: protected identity] has recently questioned this assumption by showing that the phenomenon of persistence observed in Mycobacterium smegmatis exposed to isoniazid, an antibiotic inhibiting bacterial cell wall synthesis, is not correlated with the growth rate of single cells. In other words, under the microscope, cells that are likely to die are indiscriminately cells that grew quickly or slowly. Moreover, this team has also highlighted a counter-intuitive result: at a "bactericidal" antibiotic concentration, the persistence state is not a steady state due to a static number of viable cells. It is a dynamical steady state where division and death are balanced.
Thus, bacterial growth, antibiotic-mediated killing and persistence, which were believed to be “well-understood phenomena” or “questions from the past”, yet reveal many interesting facets that are probably related to molecular noise at the single-cell level and that we propose to study. We have formulated two issues that shape our research project for a period of two years. The two following issues represent a starting point in so far as we also expect that our experimental system will serve as a generator of new questions.
- What are the dynamics of bacterial division and death, at the single cell level, when varying the concentration of antibiotics?
- Is there a link between the effectiveness of an antibiotic and the growth rate at the level of single cells ?
To answer these questions, we will grow bacteria in custom-made microfluidic devices and image them by time-lapse microscopy. We will make several such experiments by varying either the concentration of the antibiotic or the growth rate of the bacteria. The time-lapse microscopy data should allow us to properly characterize the behavior of individual cells within cell lineages and to measure several phenotypic parameters of interest. The main technical challenge at the outset of these studies will be to establish procedures to control the rates of bacterial growth and division by using continuous-flow microfluidic devices as chemostats. These custom-made devices are designed and constructed in the [2023: protected identity] lab. In conjunction with the experimental studies, we will also develop and implement deterministic and stochastic computational models of single-cell growth and division and antibiotic-mediated killing. The corresponding computational framework should (1) assist us in the understanding of experimental observations that defy intuition and (2) allow us to infer phenomenological parameters from the comparisons between experiments and in silico simulations.
The organisms that we plan to use are Mycobacterium smegmatis (a non-pathogenic organism that is phylogenetically close to the human pathogen Mycobacterium tuberculosis) and a pathogenic strain of Escherichia coli (UPEC). The corresponding infections (tuberculosis and urinary tract infection) are chronic and unusually difficult to eliminate with antibiotic therapy. Among the hypotheses proposed to explain chronicity and refractoriness to therapy, there is the phenomenon of phenotypic diversity associated with the poor effectiveness of antibiotics against slow-growing and non-growing cells. Thus, the knowledge generated from our experiments is likely to have important implications for medical microbiology. Future studies, beyond the scope of this two-year project, will attempt to relate our findings in M. smegmatis to M. tuberculosis, which is the principal organism studied by the [2023: protected identity] laboratory; however, work with M. tuberculosis, which requires Biosafety Level 3 containment, is slow and difficult compared to M. smegmatis or UPEC.
State of the art
Evolution is one of the phenomena responsible for the gradual adaptation of organisms to changes in their environments. Mutations and exchanges of genetic material increase microbial diversity but these are rare events that pass through the filter of natural selection. Bacteria have another way to adapt to their environment without direct recourse to evolution. They adapt their cellular contents (RNA, proteins, metabolites...) through a large and complex regulatory network including, among others, signal transduction, transcriptional regulation, and metabolic fluxes (Jacob and Monod 1961). Elucidating the dynamical functioning of this cellular network is a major goal of systems biology (Alon 2006). The network includes many feedback loops and the corresponding dynamics are therefore inherently nonlinear. In addition, the inherently stochastic nature of regulatory mechanisms makes bacterial behavior seem idiosyncratic: two cells that have the same genotype and the same network topology, when challenged with same perturbation, can nonetheless adopt two very distinct phenotypes. In other words, and in contrast to the "conventional wisdom", an organism's phenotype is not a rigidly deterministic and predictable outcome of the interaction of genotype with its environment. Instead, individual organisms are phenotypically plastic and their behavior is largely unpredictable.
One important source of the phenotypic diversity of single cells is related to the random Brownian motion of molecules (molecular "noise"), which introduces probabilities in the functioning of the cellular regulatory network. Asymmetric probabilities are introduced, for instance, when the cell content is partitioned during the cell division or when a transcription factor randomly binds or unbinds to its promoter. Thus, when a perturbation in the environment occurs, a population of cells can dynamically change (1) the average concentration of certain cellular components, but also (2) the single-cell distribution (wide or narrow) of these components within the population and (3) the shape of this distribution (Gaussian, Poisson, Gamma, multi-modal...).
A population of cells not only experiences the effects of molecular noise, it may also utilize noise to its advantage (Eldar and Elowitz). The regulatory network contains, for example, certain motifs found in a number that is statistically higher compared to what should be found in a random network (Alon 2007). This is the case, for example, of positive feedback loops that can generate multi-stability in the concentration of a given protein. This phenomenon has been observed in the expression of the lactose (Ozbudak, Thattai et al. 2004) and arabinose (Megerle, Fritz et al. 2008) operons in Escherichia coli and is also responsible for the bipartition into two distinct subpopulations (sporulating cells and non-sporulating cells) in Bacillus subtilis (Maamar and Dubnau 2005; Maamar, Raj et al. 2007).
From an evolutionary point of view, this phenotypic diversity could be advantageous for a population of cells in a fluctuating environment (Kussell and Leibler 2005) because it avoids that the population "puts its eggs in one basket". This diversification can be viewed as a “bet-hedging strategy” (Veening, Smits et al. 2008). Indeed, if a sudden and potentially lethal change appears in the environment, most of the cells might be killed but a few individuals might be able to persist due to their phenotypic differences. Historically, the first identified example of phenotypic diversity was the phenomenon of bacterial persistence (Bigger 1944), whereby a subpopulation of cells seemed to be refractory to the bactericidal effect of penicillin but this trait was not inherited by the progeny (Levin and Rozen 2006). Persistent cells, against which penicillin was ineffective, seemed to be in stationary phase suggesting that there were cells that no longer undergoing growth and division (Hobby, Meyer et al. 1942; Hobby and Dawson 1944). This hypothesis was confirmed when subpopulations of non-dividing E. coli cells were shown to be refractory to ampicillin due to the existence of a stochastic switch between a "normal growth" state and a "slow-growing" or "non-growing" phenotype (Balaban, Merrin et al. 2004). Until recently, the reversible adoption of a slow-growing or non-growing state has been widely regarded as a "universal" mechanism for persistence. The underlying assumption is that the bactericidal efficacy of an antibiotic is directly proportional to the growth rate of bacteria. This hypothesis was confirmed by experiments carried out in chemostat cultures, i.e., at the population level (Tuomanen 1986).
Since recent years / decades, it has become possible to focus not only on the average behavior of a population of cells, but on the behavior of each individual cell belonging to this population using instruments such as flow cytometry or microscopy (Brehm-Stecher and Johnson 2004). By performing experiments at the single-cell level, the team of Prof. [2023: protected identity], in which I wish to conduct my research, has recently questioned the assumption of a universal relationship between growth rate and efficiency of an antibiotic (Wakamoto, Dhar et al. 2013). This team was able to show that the phenomenon of persistence observed in M. smegmatis exposed to isoniazid, an antibiotic inhibiting bacterial cell wall synthesis, is not correlated with the growth rate of single cells. In other words, under the microscope, non-growing, slowly growing, and rapidly growing cells are equally likely to die or persist under antibiotic exposure. The team was also able to highlight a counter-intuitive result: at a "bactericidal" antibiotic concentration, the persistence state is not a steady state due to a static number of viable cells. Rather, it is a dynamical quasi-steady state where division and death are ongoing and balanced. In other words, at a "bactericidal" antibiotic concentration, cell division continues, thus contradicting the intuitively satisfying but nonetheless incorrect interpretation of observations made at the population level.
In sum, the relationship between bacterial growth and antibiotic-mediated killing, phenomena that were believed to be “well-understood” or “questions from the past”, may yet reveal many interesting and unexpected facets, now that we have the experimental and computational tools to explore these phenomena at the single-cell level. We propose to study these facets that are directly related to phenotypic diversity and molecular noise. For this purpose, we have formulated two issues that shape our research project for a period of two years.
Questions
What are the single-cell dynamics of bacterial division and death when varying the concentration of antibiotic?
To answer this question, we will grow bacteria in custom-made microfluidic devices and repeatedly image them by microscopy over time. We will make several such experiments by varying the concentration of antibiotic applied in the flow medium. The microscopy data obtained should allow us to properly characterize individual cells within well-defined cell lineages and to measure several phenotypic parameters of interest.
By titrating down the concentration of a "bactericidal" antibiotic, one can reach a concentration where the effects of the antibiotic appear to be “bacteriostatic” rather than “bactericidal”. At this concentration, intuition makes us represent a population that can no longer divide but resumes growth if the antibiotic is removed from the medium. This view could be misleading. Indeed, by titrating the antibiotic, we could imagine that the "growth rate" might increase while the "killing rate" might remain constant, rather than vice versa, as is generally assumed. Thus, as observed with the "bactericidal" state, the "bacteriostatic" state could be a dynamical steady state where growth and death are in balance.
The current dogma in medical microbiology is that antibiotic therapy arrests bacterial growth and division and hence the evolutionary mechanisms behind the emergence of antibiotic-resistant strains. If our conjecture is true (i.e., cells continue to divide in the presence of antibiotics), this could have important implications for medicine. Indeed, this would mean that the wheel of evolution could continue to turn even during the treatment phase of patients, as antibiotic concentrations in the tissues rise and fall between doses, providing a plausible explanation for the rapid emergence and fixation of antibiotic resistance due to heritable mutations.
Is there a link between the bacterial growth rate and the effectiveness of an antibiotic?
This question is a continuation of the previous one and therefore requires similar experiments. We will use custom-made microfluidic devices as chemostats to control the growth rate of the bacteria by titrating the concentration of an essential nutrient in the flow medium. We will then assess the relationship between bacterial growth rates and rates of antibiotic-mediated killing and persistence by adding an antibiotic to the flow medium and imaging the bacteria by time-lapse microscopy. The microscopy data obtained should allow us to precisely quantify the impact of the growth/division rates of single cells on the effectiveness of the antibiotic. Importantly, this work will focus on the relationship between rates of growth and death at the single-cell level, which has not, to the best of our knowledge, been analyzed in any organism.
Materials and methods
Choice of the organism
Our choice is currently focused on two distinct organisms: Mycobacterium smegmatis and uropathogenic Escherichia coli (UPEC). It has not yet been decided if the experiments would take place systematically and in parallel with these two types of organisms or if one of the two would be finally discarded. Similarly, the choice of antibiotics has not yet been arrested, although we will probably focus on antibiotics that are effective against both organisms, e.g., streptomycin, rifampicin, beta-lactams (specifically, beta-lactams such as faropenem, which are resistant to hydrolysis by beta-lactamases).
The host laboratory has extensive experience in the use of these bacteria for microfluidic cultivation, time-lapse imaging, and genetic engineering. M. smegmatis has the advantage of being a non-pathogenic strain that can be manipulated at the bench without any special protection. The knowledge obtained can be, at least partially, extrapolated to the phylogenetically related M. tuberculosis, which is an important human pathogen. Uropathogenic E. coli (UPEC) is responsible for 90% of urinary tract infections and represents a major public health problem. From the experimental point of view, UPEC has the advantage of having an intrinsic growth rate that is much higher than that of M. smegmatis and a larger number of potentially useful tools are available for UPEC (e.g., overexpression plasmids, transcriptional fusion constructs, etc.). However, UPEC must be handled under more restrictive conditions because of its pathogenicity (Biosafety level 2). The [2023: protected identity] lab is fully equipped for work with both Biosafety Level 2 and Biosafety Level 3 organisms.
A common point between M. tuberculosis and UPEC is the chronicity often observed in the corresponding infections and the related difficulty of achieving an effective treatment that completely eradicates the pathogen (McKinney 2000; Gomez and McKinney 2004; Blango and Mulvey 2010). Among the hypotheses proposed to explain this chronicity, there is the phenomenon of persistence due to phenotypic diversity together with the poor effectiveness of antibiotics when the growth rate is low – for example, in biofilms (Lewis 2005) or when bacteria enter human cells. Thus, the proposed project to study the phenotypic diversity of division and death in the presence of antibiotics could generate knowledge that will be available/usable in the context of medical microbiology.
Main experiment
The experiments that we propose will be done by culturing cells in custom-made microfluidic devices and imaging them by time-lapse fluorescence microscopy. The laboratory of Prof. [2023: protected identity] has all of the necessary expertise and facilities for the manufacture of microfluidic devices and has 6 fully motorized fluorescence microscopes for automated imaging of single cells for periods of up to 6-8 weeks. Thus, the technologies and procedures needed to carry out the proposed work are already well established and indeed routine in the host laboratory.
On the other hand, a large part of the preliminary experimental work will consist of developing tools and methods for using microfluidic chemostats to tune the growth rate of cells during continuous time-lapse imaging. Among the strategies we could pursue to finely control the growth rate of microfluidic cultures, we currently consider the following (from the simplest to the most complex):
- The use of carbon/nitrogen sources of varying quality
- The use of limiting carbon / nitrogen concentrations (“fed-batch” culture)
- The implementation of an external feedback loop (Uhlendorf, Miermont et al. 2012), where a computer measures the growth rate in real time and, via an action on a pump, dynamically changes the concentration of the carbon/nitrogen sources to tune the growth rate (Figure 1).
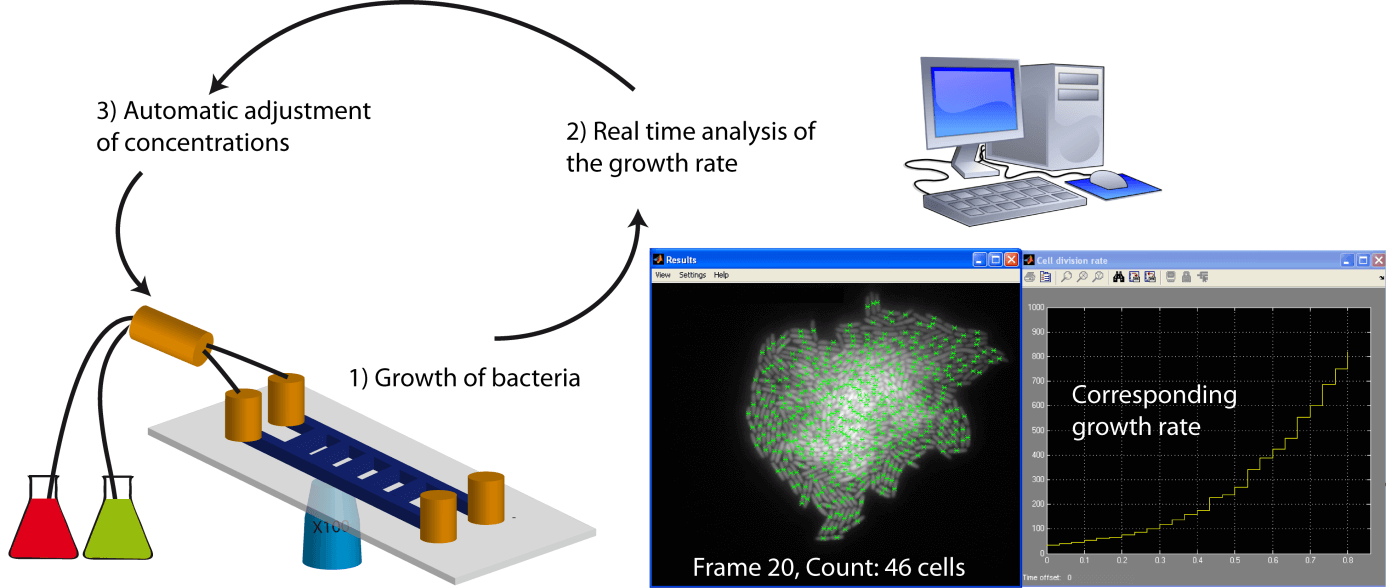
Data processing
The [2023: protected identity] laboratory uses a combination of automated algorithms and hand editing to process image stacks obtained by time-lapse microscopy, and is actively involved in the development of "new and improved" algorithms for automated image processing, in collaboration with the Biomedical Imaging Laboratory headed by Prof. Michaël Unser (EPFL, School of Engineering). Also, new programs, often working within Matlab, ImageJ, or Labview, regularly appear and improve the automated image processing, saving valuable time (Meijering, Dzyubachyk et al. 2012). These programs allow, for example, the automated segmentation of images and temporal tracking of single cells in order to generate lineages and to extract parameters of interest. With the aim of constantly improving our procedures for data analysis, we will explore these new programs and use the easier, the most efficient and modular ones. The availability of the source code is a prerequisite, given that we will certainly need to adapt these programs to our experimental conditions and questions.
The parameters of interest that we will try to extract from the images remain to be defined precisely since it will be easier to identify them once we have the data. Nevertheless, we will certainly extract and analyze the following:
- The single-cell lineages (and therefore the identification of division and death events, the mother and daughter cells)
- The single-cell rates of growth, division, and death
- The general phenotypic parameters of single cells (area, shape, etc.)
- The single-cell fluorescence intensity (for experiments involving fluorescent reporters).
Computational Modeling
We will develop different classes of models (1) to assist us in understanding experimental observations that defy intuition, and (2) to compare experimental data with data generated by in silico simulations in order to infer certain parameters.
We will write simple deterministic models of bacterial growth and division based on existing work in this area (Stephen 2010). Stochastic models, more suitable to simulate the process of division and death at the single cell level, will also be implemented, by adapting the Gillespie algorithm to bacterial growth (Gillespie 1977). The modeling framework will be developed using Matlab, either by means of the SimBiology toolbox or through "home-made" programs (Figure 2), which will make the resulting programs more "user-friendly" and accessible to non-specialists.
The comparison between data derived from experimentation and from computational modeling will aim to infer some phenomenological parameters such as those describing the potential impact of the growth rate on the effectiveness of an antibiotic. To perform this task, we will use classical tools that search global optima such as genetic algorithms.
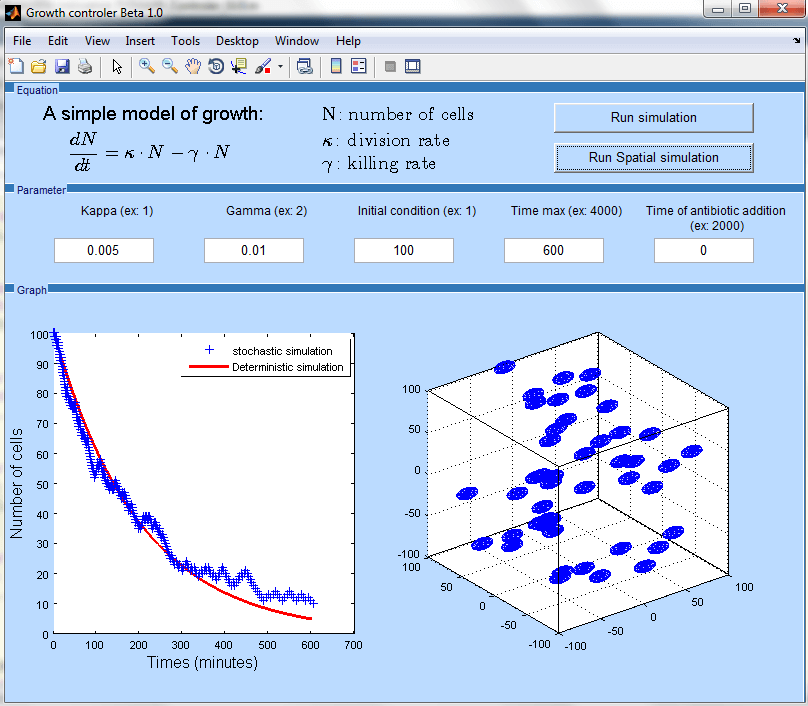
Milestone
Setting up a schedule of work progress is usually quite difficult in the field of research as it is difficult to reliably predict the problems that will be encountered. Let’s still attempt to make these predictions, even though I must confess that I often underestimate how long “things” take.
Familiarization with the biological material and the instruments
First, I will have to familiarize myself with the specific culture conditions for M. smegmatis and uropathogenic Escherichia coli (UPEC). Second, I will have to learn specific precautions for handling UPEC. I will also learn how to design and construct my own microfluidic chips in order to gain independence in this area, which will allow me to transplant this technology to my next lab in the future after I complete my postdoc and leave the [2023: protected identity] lab. Finally, I'll need to familiarize myself with the motorized/automated microscopes used in the laboratory. These points (except the design and manufacture of microfluidic chips) should be achieved fairly quickly (on the order of weeks to months).
Optimization of the image processing
One point that looks essential to me is to keep the time spent on processing images to a reasonable level, i.e., of the same order of magnitude as the time required to perform the experiments themselves. Indeed, the time spent to process data should not become the "Achilles heel” that limits the number of experiments that are feasible. To avoid this, one needs efficient software that automates the image processing as much as possible to minimize the intervention of the experimenter. The time required to establish an optimal procedure will depend on:
- The already existing procedures used in the laboratory.
- The existence of potentially interesting new programs.
- Our ability to understand and adapt the source code to suit our goals.
Ideally, this time should not exceed a few months.
Computational modeling
The development of the initial modeling framework should be relatively rapid. Indeed, models of growth, division, and death should be relatively simple to develop since the parameters are well defined and limited in number. For the same reasons, the comparison of the experimental data with the simulation data in order to infer parameters of interest should not be too problematic. The time spent on this part should not exceed a few months.
Control of the growth rate
Techniques for precise control of the growth rate of cells grown in microfluidic devices have not yet been developed in the [2023: protected identity] laboratory. And this technical advance might be less trivial than it seems. Thus, it is difficult to predict how long it will take to transform the microfluidic device into an effective chemostat for controlling the growth rate of microfluidic cultures. Searching in a set of experimental conditions (variation of the carbon or nitrogen sources and their concentrations) would probably required a few months to identify a robust protocol. Implementing an external feedback loop (computer-pump) may require more work (including programming) and will mainly depend on the capability to analyze images and extract parameters in real time. Several months may be needed to get a robust procedure able to finely tune the growth rate in real time in order, for instance, to keep it constant. Note that it is likely that the modeling framework will actively contribute to the functioning of the feedback loop.
Main experiments
The experiments corresponding to our two main questions (studying the dynamics of division and death of single cells at different growth rates and antibiotic concentrations) should be performed relatively quickly (a few months) if the above procedures have been properly optimized. Although we have formulated two specific questions, we expect that our system will also serve as a generator of new questions. Our intuition (which often prefers to deal with population means rather than with frequency distributions) is unable to predict the results that we are going to obtain and thus the corresponding issues that may emerge.
Controls and formatting of the results
Whatever the results obtained, they undoubtedly will require controls that are difficult to predict and that often represent a significant part of the work. The formatting of the results and the drafting of a potential publication are also time consuming. We reasonably allocate at least six months to perform this part of the work.
Synthesis of the milestones
- Learning the specific laboratory procedures, optimizing the image processing, and modeling the bacterial growth: 6 months.
- Controlling the growth rate under the microscope: 6 months.
- Experiments related to our two main questions: 6 months.
- Controls and formatting of the results: 6 months.
Expected impact and contribution to the system biology research in Switzerland by this project /fellowship
The main contribution of our research will correspond to the quantitative single-cell analysis of the relationship between (i) rates of growth and division, which will be controlled using microfluidic chemostats, and (ii) antibiotic-mediated killing and persistence. At first glance, this might appear to be a question that has already been addressed in the past, but surprisingly, to the best of our knowledge this relationship has not been systematically addressed at the single-cell level in any organism. The marked cell-to-cell variation in growth rates of single cells, which is likely to be directly connected to the so-called extrinsic noise, could potentially have a strong impact on the efficiency of a given regulatory function. Thus, measuring the variation in growth and division rates of single cells as a function of time and consolidating this information within computational models may provide a more accurate picture of the functioning of physiological networks and the phenomenon of phenotypic diversity. Thereby, these goals are directly related to system biology. Construction of computational models based on the parameters that will be measured in our experiments will provide a framework both for interpreting the results of our experiments and for generating new hypotheses that can be tested by further experimentation. Thus, I see my postdoc project as a cyclical and interactive process of wetlab experimentation and computational modeling.
Justification of the Systems Biology approach
From a theoretical point of view, the growth and division rates of bacteria critically depend on the functioning of the underlying regulatory networks and vice versa. Cell-to-cell variation of the growth/division rates, which is readily measurable by time-lapse microscopy, may be “programmed” in the genome and integrated in the functioning of the cell's regulatory networks, which is a major focus of systems biology. From a technical point of view, the tools and methods that we propose to develop and apply, which include time-lapse microscopy of single cells and computational modeling, are clearly within the domain of systems biology.
Significance of the planned research for the scientific community and eventual users (private industry, economy, medicine)
The significance of our planned research for the systems biology community has been explained above. The second and at least equally important contribution is relative to the goals of medicine. Indeed, the organisms that we have chosen are not classical model organisms of systems biology, such as Escherichia coli MG1655 or Saccharomyces cerevisiae. Instead, we have chosen to perform experiments directly on either a pathogenic strain of E. coli (UPEC) or on M. smegmatis, which is phylogenetically close to the human pathogen M. tuberculosis.
The reason for this choice of organisms is simple: phenotypic diversity is thought to be the main reason explaining chronicity observed either in urinary tract infection (UPEC) or in tuberculosis. More specifically, phenotypic diversity is thought to explain the phenomenon of persistence to antibiotics that prevents the total eradication of the pathogen. This is why the major part of our research project focuses on the growth rates of individual cells in the presence of antibiotics. From a medical perspective, the experiments would be directly performed on “interesting strains” avoiding time-consuming “transposition” steps. Therefore, our results will further the understanding of the phenomenon of bacterial persistence and may directly benefit medicine. The laboratory of Prof. [2023: protected identity] has extensive experience in the sharing of these distinct objectives, i.e., systems biology and medical applications. The microscopes that I will use in my time-lapse experiments are already located in dark rooms equipped for work with Biosafety Level 2 (UPEC) and Biosafety Level 3 (M. tuberculosis) organisms and the procedures for microfluidic culture and long-term time-lapse imaging of these organisms are already established.
References
- Alon, U. (2006). An introduction to system biology, Chapman and Hall/CRC.
- Alon, U. (2007). "Network motifs: theory and experimental approaches." Nat Rev Genet 8(6): 450-61.
- Balaban, N. Q., J. Merrin, et al. (2004). "Bacterial persistence as a phenotypic switch." Science 305(5690): 1622-5.
- Bigger, J. (1944). "Treatment of staphylococcal infections with penicillin by intermittent sterilisation." Lancet.
- Blango, M. G. and M. A. Mulvey (2010). "Persistence of uropathogenic Escherichia coli in the face of multiple antibiotics." Antimicrob Agents Chemother 54(5): 1855-63.
- Brehm-Stecher, B. F. and E. A. Johnson (2004). "Single-cell microbiology: tools, technologies, and applications." Microbiol Mol Biol Rev 68(3): 538-59, table of contents.
- Eldar, A. and M. B. Elowitz "Functional roles for noise in genetic circuits." Nature 467(7312): 167-73.
- Elowitz, M. B., A. J. Levine, et al. (2002). "Stochastic gene expression in a single cell." Science 297(5584): 1183-6.
- Gillespie (1977). "Exact stochastics simulation of coupled chemical reactions."
- Gomez, J. E. and J. D. McKinney (2004). "M. tuberculosis persistence, latency, and drug tolerance." Tuberculosis (Edinb) 84(1-2): 29-44.
- Hobby, G. L. and M. H. Dawson (1944). "Effect of Rate of Growth of Bacteria on Action of Penicillin." Proceedings of the Society for Experimental Biology and Medicine. Society for Experimental Biology and Medicine (New York, N.Y.) 56(2): 181-184.
- Hobby, G. L., K. Meyer, et al. (1942). "Observations on the Mechanism of Action of Penicillin." Proceedings of the Society for Experimental Biology and Medicine. Society for Experimental Biology and Medicine (New York, N.Y.) 50(2): 281-285.
- Jacob, F. and J. Monod (1961). "Genetic regulatory mechanisms in the synthesis of proteins." J Mol Biol 3: 318-56.
- Kussell, E. and S. Leibler (2005). "Phenotypic diversity, population growth, and information in fluctuating environments." Science 309(5743): 2075-8.
- Levin, B. R. and D. E. Rozen (2006). "Non-inherited antibiotic resistance." Nat Rev Microbiol 4(7): 556-62.
- Lewis, K. (2005). "Persister cells and the riddle of biofilm survival." Biochemistry (Mosc) 70(2): 267-74.
- Maamar, H. and D. Dubnau (2005). "Bistability in the Bacillus subtilis K-state (competence) system requires a positive feedback loop." Mol Microbiol 56(3): 615-24.
- Maamar, H., A. Raj, et al. (2007). "Noise in gene expression determines cell fate in Bacillus subtilis." Science 317(5837): 526-9.
- McKinney, J. D. (2000). "In vivo veritas: the search for TB drug targets goes live." Nat Med 6(12): 1330-3.
- Megerle, J. A., G. Fritz, et al. (2008). "Timing and dynamics of single cell gene expression in the arabinose utilization system." Biophys J 95(4): 2103-15.
- Meijering, E., O. Dzyubachyk, et al. (2012). Chapter nine - Methods for Cell and Particle Tracking. Methods in Enzymology, Academic Press. Volume 504: 183-200.
- Ozbudak, E. M., M. Thattai, et al. (2004). "Multistability in the lactose utilization network of Escherichia coli." Nature 427(6976): 737-40.
- Stephen, J. H. (2010). Exponential growth of bacteria: Constant multiplication through division, AAPT. 78: 1290-1296.
- Tuomanen, E. (1986). "Phenotypic tolerance: the search for beta-lactam antibiotics that kill nongrowing bacteria." Rev Infect Dis 8 Suppl 3: S279-91.
- Uhlendorf, J., A. Miermont, et al. (2012). "Long-term model predictive control of gene expression at the population and single-cell levels." Proc Natl Acad Sci U S A 109(35): 14271-6.
- Veening, J. W., W. K. Smits, et al. (2008). "Bistability, epigenetics, and bet-hedging in bacteria." Annu Rev Microbiol 62: 193-210.
- Wakamoto, Y., N. Dhar, et al. (2013). "Dynamic persistence of antibiotic-stressed mycobacteria." Science 339(6115): 91-5.