Le bruit en biologie
Les origines du bruit
Deux jumeaux (ou deux clones de brebis) diffèrent en apparence et en comportement. Bien qu'ayant exactement le même génome, ils vont faire des choix différents durant leur vie: ils conservent heureusement leur libre arbitre. Les choses fonctionnent de la même manière dans une population de cellules clonales (ayant le même génome). En effet, des cellules identiques génétiquement exposées au même environnement/milieu peuvent cependant montrer des variations significatives dans leur contenu cellulaire (protéine, ARN, métabolite etc...) et donc montrer des différences sur le plan phénotypique: 1 génome, 1 milieu, plusieurs phénotypes. Cette variabilité est liée à la nature stochastique de l'expression des gènes. Cette dernière est elle-même due au déplacement aléatoire des molécules selon le mouvement brownien ce qui injecte des probabilités dans les phénomènes observés. Ainsi la variation stochastique dans l'expression des gènes est appelée bruit et c'est un déterminant clé des variations phénotypiques observées entre cellules clonales. Quand une molécule X est présente en très nombreux exemplaires dans la cellule, les effets de X sont facilement et correctement prédits par un modèle déterministe qui représente le comportement moyen de l'ensemble des exemplaires de X. A l'inverse quand la molécule X n'est présente qu'en quelques exemplaires, les effets stochastiques/le bruit deviennent prédominants.
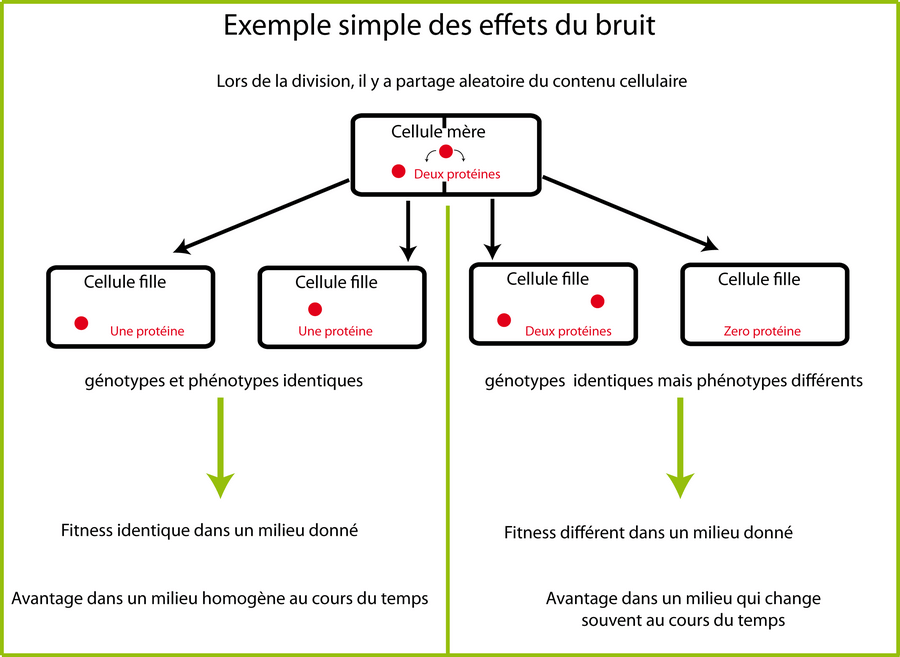
Prenons le cas d'une protéine présente en 10 exemplaires dans une cellule mère1 . Lors de la division, chaque cellule fille héritera en moyenne de 5 exemplaires de cette protéine. Mais en réalité, la répartition n'est pas une simple division par deux: elle suit une loi de Gauss (forme de cloche centrée sur la moyenne). Autour de cette moyenne de 5 exemplaires se produiront des situations très diverses et il y a une certaine probabilité (faible) qu'une cellule fille hérite des 10 exemplaires et que l'autre n'en obtienne aucun. Si on place alors judicieusement une boucle de rétroaction positive dans notre système, on peut maintenir cette différence éternellement: les cellules filles de la cellule qui n'a hérité d'aucun exemplaire resteront "OFF" comme leur mère et les cellules filles de la cellule qui a hérité des 10 exemplaires resteront "ON". On comprend donc bien qu'un état phénotypique lié au bruit puisse se transmettre de génération en génération: il s'agit d'un cas particulier d'héritage épigénétique.
Je voudrais cependant tempérer ici l'idée que le processus de division est asymétrique à cause du seul hasard. En effet, l'équipe de François Taddei a montré que les cellules filles qui héritent des pôles "vieux" arborent une diminution du taux de croissance (Stewart et al. 2005): elles vieillissent puis elles meurent. Il semblerait que la raison à ce résultat étonnant soit l'accumulation d'agrégats protéiques dans les pôles les plus vieux au cours des divisions. Les cellules déploieraient donc une stratégie de répartition asymétrique des agrégats protéiques pour perpétuer la population au détriment de cellules âgées (Lindner et al. 2008). Ce résultat démolit l'idée intuitive que toutes les cellules d'une population comme E. coli se divisent de manière infinie tant qu'il y a du milieu frais.
L'intérêt du bruit
Le bruit dans l'expression des gènes est souvent perçu par les biologistes de manière négative: le bruit provoquerait des effets néfastes et la cellule aurait appris, au cours de l'évolution, à le combattre ou du moins à le contrôler. Mais le bruit n'est pas uniquement nuisible: une population de cellules peut l'utiliser pour accroitre son fitness. En effet, l'hypothèse la plus logique pour expliquer pourquoi les bactéries exhibent des variations phénotypiques c'est qu'il s'agit d'une stratégie dite "de pari " (bet-hedging strategy): les variations phénotypiques permettent à la population de ne pas mettre tous ses oeufs dans le même panier. Si un changement brusque et violent apparait dans l'environnement, la plupart des cellules seront peut être tuées mais quelques unes seront peut être en mesure de résister grâce à leur différence de phénotype. Un des exemples le plus connu de stratégie de pari est le phénomène de persistance bactérienne, identifié la première fois dans les années 40 (Bigger 1944). Les cellules dites persistantes sont résistantes aux antibiotiques qui s'attaquent aux cellules en division. Autrement dit ces cellules sont dans un état transitoire d'arrêt de croissance ce qui les protège des antibiotiques alors même que leur génome est identique à celui des autres cellules sensibles aux antibiotiques. Le "switch" entre "croissance normale" et "état de persistance" est stochastique par nature: 1 cellule sur 10, sur 100 ou sur 1000 est, par exemple, dans cet état et si un antibiotique arrive, toutes les cellules seront tuées sauf celle-ci. Si l'antibiotique finit par disparaitre, certaines cellules persistantes "switcheront" à nouveau vers un mode de "croissance normale" ce qui entrainera le retour de la population bactérienne. Cette population sera à nouveau composée de cellules sensibles aux antibiotiques et de cellules persistantes. Un autre exemple très classique de stratégie de pari est le phénomène de sporulation chez Bacillus Subtilis. La sporulation est un processus bistable car deux sous-populations peuvent être distinguées dans une population clonale de cellules en phase stationnaire: les spores (très résistants aux stress environnementaux) et les cellules "non-sporulantes" capables de repartir en croissance exponentielle plus rapidement si du milieu de croissance "frais" réapparait.
De manière plus générale, on comprend, avec ces exemples, que dans des conditions environnementales changeantes, la production d'une descendance avec des phénotypes variables assure qu'au moins 1 des descendants aura le phénotype approprié dans un environnement donné (ce descendant "fitte" bien avec le milieu). C'est une stratégie de répartition des risques qui a pour conséquence que les descendants ne sont pas tous adaptés de manière optimale à l'environnement futur. Ainsi, dans un environnent très fluctuant, le fitness global d'une population hétérogène peut être supérieur à celui d'une population homogène. A l'inverse, dans un milieu constant, une population homogène aura toujours un fitness supérieur. En fait, il est fort possible que la répartition optimale des phénotypes mime les statistiques de changements environnementaux. Ainsi la variation phénotypique due au bruit n'est pas seulement un handicap ou un défaut: c'est un paramètre qui peut probablement être "tuné / sélectionné " par l'évolution en fonction de la fréquence des changements environnementaux.
Notez que chez les organismes supérieurs (le ver C. elegans, la drosophile, l'homme...), le bruit ne permet pas seulement une meilleure adaptation aux environnements fluctuants, il intervient également dans le processus de développement. L'hétérogénéité (la simple gaussienne) présente dans une population clonale de cellules non différenciées pourrait subir des mécanismes d'amplification orientant petit à petit l'expression de gènes de chaque cellule dans une voie de différentiation particulière.
Le contrôle du bruit
Comment la cellule contrôle-t-elle le bruit ? Certains mécanismes de rétrocontrôle pourraient avoir évolué spécifiquement pour minimiser ou amplifier l'impact des variations stochastiques dans l'expression des gènes. On cite souvent la boucle de rétroaction négative comme système capable de réduire le bruit. Pour tester cette hypothèse, des chercheurs ont fusionné le gène codant pour le facteur de transcription TetR avec celui codant pour la GFP. Cette protéine de fusion réprime l'expression de son propre gène (via le promoteur tet). Les chercheurs ont ensuite mesuré la distribution de fluorescence des cellules et montré que cette distribution est plus étroite en présence de la boucle de rétroaction que sans cette dernière (Becskei and Serrano 2000).
A l'inverse, une cellule peut amplifier les effets du bruit en utilisant une boucle de rétroaction positive. En faisant varier la force de la boucle de rétroaction, on peut même transformer une réponse graduelle en une réponse binaire où les cellules expriment un gène soit fortement soit faiblement (Isaacs et al. 2003). A l'échelle de la population, ce comportement d'interrupteur peut résulter en une distribution bimodale dans l'expression du gène: quand on observe ce type de pattern, on parle en général de bistabilité (voir le chapitre sur les systèmes dynamiques). Ce phénomène de bistabilité induit par une boucle de rétroaction positive, a été décrit pour la première fois dans les années 50 par Novick et Weiner avec l'expression de la β-galactosidase (Novick and Weiner 1957). Voici une phrase limpide extraite de leur publication:
"It was difficult to understand this result on the assumption that each bacterium has about the same enzyme content. We were able to show that this assumption does not apply at low inducer concentrations. We discovered that at the low inducer concentrations used in these experiments the population consists essentially of individual bacteria that are either making enzyme at full rate or not making it at all [...] .This can be understood on the following basis. When inducer is added to a culture of growing bacteria, there is a certain chance, determined by the inducer concentration, that a given bacterium will produce its first permease molecule. Once a bacterium has one permease molecule, the internal inducer concentration is raised, and the probability of the appearance of a second permease molecule is increased. In this sense the induction of permease in the individual bacterium is an autocatalytic process 2 , and, within a short time after the appearance of its first permease molecule, the bacterium becomes fully induced, synthesizing both permease and galactosidase at maximum rate. Because the transition is accomplished so rapidly, the relative number of bacteria at an intermediate state of induction is small."
Pour obtenir un réseau capable de générer des multi stabilités, il faut en général:
- soit que le système exhibe des cinétiques non linéaires. Pour les facteurs de transcription, la non-linéarité peut survenir lors de liaisons coopératives sur l'ADN.
- soit que le système exhibe une ou des boucles de rétroaction positives (ou que le système exhibe un nombre pair de boucles de rétroaction négative).
Une des caractéristiques classiques de la bistabilité est le phénomène d'hystérèse. L'hystérèse se réfère à la situation dans laquelle la transition d'un état à un autre requiert l'induction (ou levée d'induction) d'un niveau plus fort que ce qui se passe lors de la transition dans le sens inverse. Ceci génère des caractéristiques de mémoire qui rendent la réponse d'une cellule à une perturbation donnée dépendante de son histoire récente.
Il faut garder à l'esprit que le concept de robustesse d'un réseau peut revêtir deux notions bien distinctes:
- la robustesse à des petites variations dans la valeur des paramètres (à rapprocher de la sensibilité aux conditions initiales et du fameux effet papillon). Ce type de robustesse n'a pas besoin d'un modèle stochastique pour être étudié: un modèle déterministe suffit.
- la robustesse au bruit: comment une cyanobactérie comme Synechococcus elongatus fait-t-elle pour maintenir constante la fréquence de ses oscillations circadiennes ? Des chercheurs ont pu montrer que la persistance d'oscillations stables (sur plusieurs mois) chez ces bactéries n'est pas due à un phénomène de synchronisation des oscillateurs par communication intercellulaire. La forte stabilité temporelle est encodée dans le réseau intracellulaire: c'est une propriété de la cellule (Mihalcescu et al. 2004). Comment une telle stabilité peut-elle exister malgré la présence de fluctuation moléculaire ? Comment le réseau circadien peut-il être si résistant au bruit biochimique ? Vous voyez que cette robustesse au bruit n'est pas exactement la même que celle relative aux petites variations dans la valeur des paramètres. En effet, ici, un modèle stochastique est indispensable pour comprendre cette robustesse.
Utiliser la position relative des gènes sur l'ADN
L'équipe de Johan Elf a construit une protéine "LacI--YFP" en fusionnant un gène codant pour le lac represseur (lacI) et un gène codant pour une protéine fluorescente (yfp). En modifiant la force du promoteur controlant la transcription de ce gène, cette équipe arrive à limiter le nombre de protéines LacI--YFP à 3 exemplaires en moyenne par cellule. En utilisant un microscope à fluorescence, les auteurs arrivent à repérer un exemplaire unique du facteur de transcription fixé sur son site spécifique sur l'ADN (le lac operateur): on parle de "single molecule microscopy" car on repère une tache de fluorescence à un endroit précis dans la cellule. Bien sûr lorsque les chercheurs ajoutent de l'IPTG, le facteur de transcription se détache et diffuse dans la cellule: on perd alors la faculté de le localiser et les images de microscopie montrent une fluorescence diffuse dans toute la cellule. Un exemplaire LacI--YFP dans une cellule met environ 360 secondes pour trouver son site spécifique sur l'ADN et s'y fixer. Il passe environ 90% du temps à diffuser le long de l'ADN de manière non spécifique (diffusion 1D) et 10% du temps à effectuer des translocations en 3D d'un segment d'ADN à l'autre en passant par le cytoplasme.
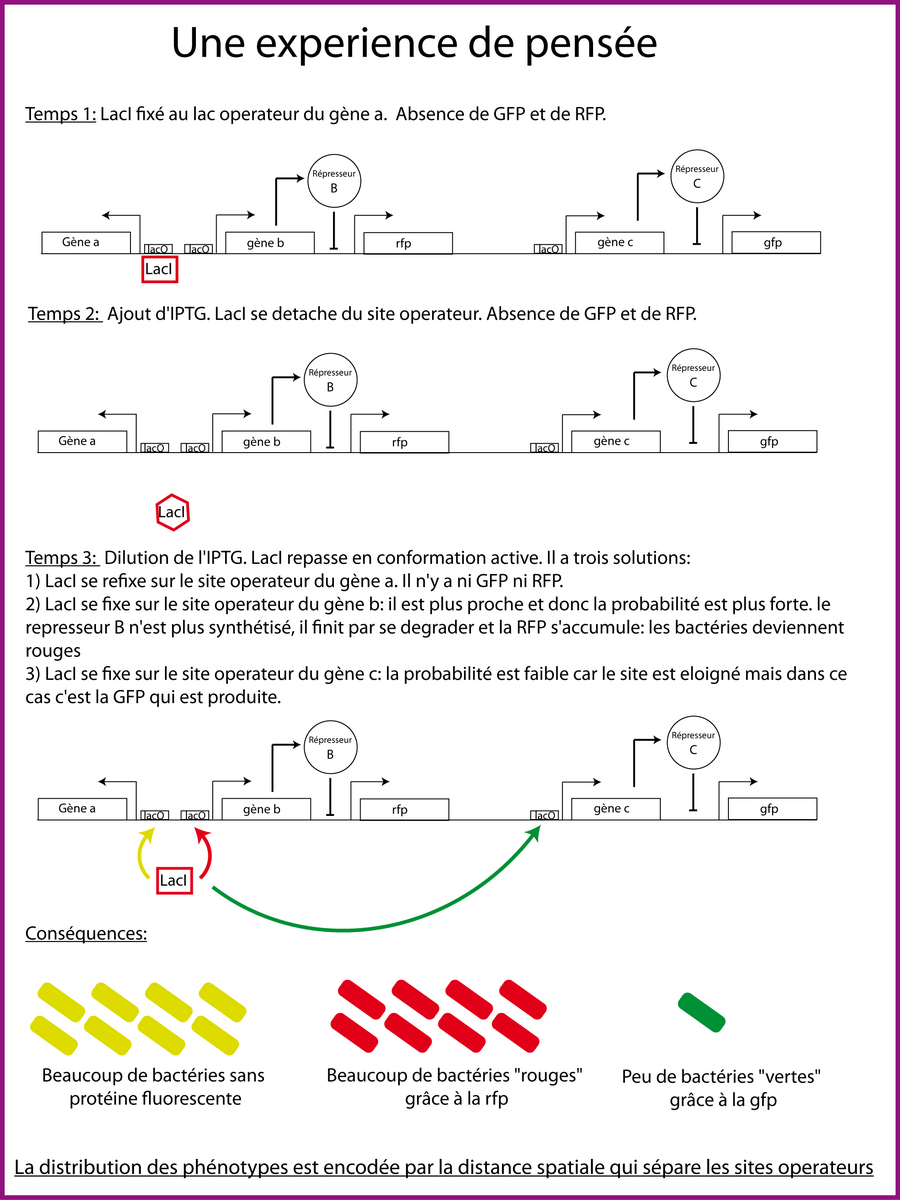
Je vous propose maintenant, à partir de ces informations, une petite expérience de pensée (figure 2) dont j'ai eu l'idée après avoir lu un article de Jean-Jacques Kupiec dans Pour la science (Kupiec 2009). Nous savons que l'effet du bruit sur l'expression de gènes est d'autant plus marqué que le nombre de molécules est restreint: considérons donc une seule molécule LacI dans la cellule mais 3 sites operateurs identiques. Le premier site est le site sur lequel est fixée la molécule LacI au début de l'expérience. Le deuxième site est très proche du premier site: par exemple à 200pb. Ce site réprime l'expression d'un gène réprimant l'expression de la RFP (Red Fluorescent Protein) lorsque LacI y est fixé. Le dernier site est beaucoup plus loin sur le chromosome (à plus de 1 million de pb) et on imagine que la distance réelle est également importante (quelques centaines de nanomètres) ce qui n'est pas forcement le cas à cause du superenroulement de l'ADN. Ce site réprime l'expression d'un gène réprimant l'expression de la GFP (Green Fluorescent Protein) lorsque LacI y est fixé. L'expérience de pensée débute en supposant qu'on a une population de 1000 cellules toutes ayant LacI sur le premier site operateur. Je rajoute de l'IPTG à une concentration suffisante ce qui libère immédiatement LacI du premier site. Puis on rajoute au bout d'un temps judicieusement choisi (entre 1 et 1000 secondes) un grand volume de milieu pour diluer l'IPTG et rendre LacI à nouveau actif. Ma question est la suivante: la probabilité que LacI se fixe au deuxième site (plus proche) est-elle supérieure à la probabilité de fixation au troisième site plus éloigné ? Autrement dit: y aura-t-il beaucoup plus de cellules rouges que de cellules vertes ? Ma prédiction est que la réponse est oui et cela signifie qu'on peut utiliser la distance relative sur l'ADN pour contrôler l'expression d'un gène. On peut encoder de l'information dans l'ADN en utilisant la distance physique qui sépare les gènes. Cela peut sembler trivial mais cela a des conséquences lorsqu'on réfléchit sur les analogies entre cellules et ordinateurs. En effet, cela signifie qu'on peut encoder une information dans l'ADN non plus uniquement en choisissant la valeur d'un nucléotide (A, T, C, G) mais également en choisissant la distance physique qui le sépare d'un autre nucléotide. Or mon hypothèse est que cela est impossible dans une machine de Turing. Je reconnais que la question est un petit peu abstraite, je ne sais pas si elle a un quelconque intérêt et depuis quelque temps, j'ai un doute. J'y reviendrai peut être un jour.
Les méthodes expérimentales pour étudier le bruit
Je vois essentiellement deux techniques permettant de mesurer les variations d'expression génique dans une population des cellules:
- La cytométrie en flux. C'est une technique qui permet de faire défiler des particules (par exemple des bactéries) à grande vitesse dans le faisceau d'un laser, en les comptant et en les caractérisant. Parmi les paramètres récoltés peuvent se trouver l'aire, le facteur de circularité (sur lequel je vais revenir) ou la fluorescence moyenne de chaque cellule. Notez un point qui me semble toujours extraordinaire: certains cytomètres en flux sont équipés d'un trieur. Prenons un exemple: vous faites passer dans votre cytomètre 100 millions de cellules "vertes" (GFP) mélangées à 100 millions de cellules "rouges" (RFP). Après l'illumination de chaque cellule par le laser, le trieur oriente chaque cellule dans un compartiment ou un autre en fonction des paramètres récoltés (la fluorescence) qui sont quasi-immédiatement disponibles. Cela vous permet de séparer vos deux populations rouges et vertes puis de les récupérer.
- La cytométrie en image. C'est une technique dont l'instrument principal est le microscope. Le chercheur acquiert des images de ses cellules (en contraste de phase et/ou en fluorescence) puis il fait tourner un algorithme qui détecte les cellules sur les images et en extrait les paramètres (comme la cytométrie en flux): l'aire, le facteur de circularité ou la fluorescence par exemple.
Avec ces deux techniques, on obtient des distributions. Par exemple, la distribution de fluorescence moyenne des cellules ou la distribution des aires des cellules. On peut ensuite "fitter" ces données de distribution avec un modèle stochastique (que nous aborderons plus loin) pour identifier les paramètres d'un modèle par exemple. La cytométrie en image est globalement plus chère que la cytometrie en flux cependant elle dispose d'un avantage de poids: elle permet à tout moment d'effectuer un contrôle visuel sur une sous-population de cellules, ce qui peut s'avérer rassurant pour l'interprétation les résultats.
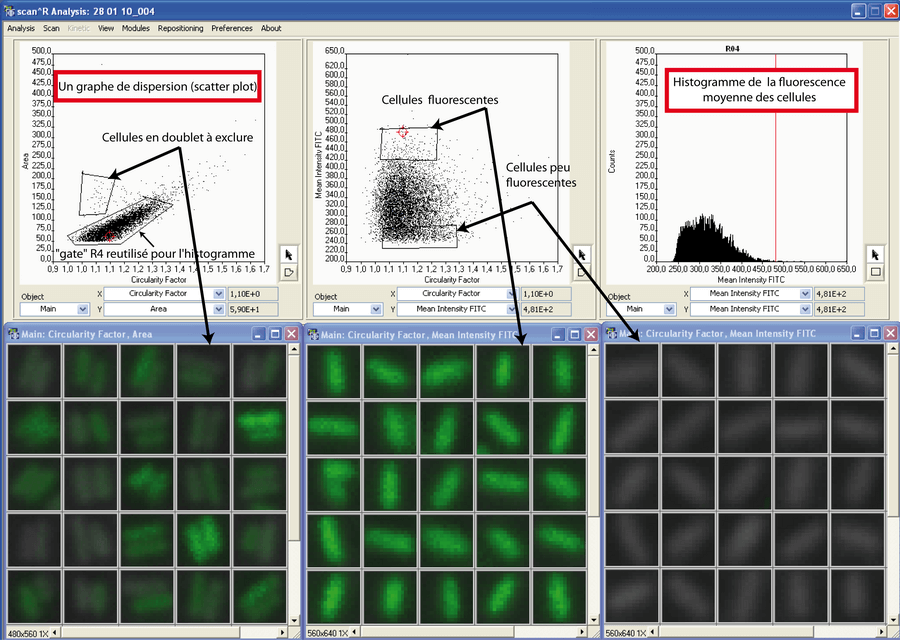
Il y a un point technique que je souhaite aborder. Il peut intéresser toute personne confrontée à des images de cellules et qui souhaiterait détecter puis extraire les paramètres à l'aide d'un petit programme "home-made". Cette personne pourrait développer son algorithme "d'image processing" et se rendre compte qu'il souhaite exclure les particules inintéressantes, par exemple, les doublets de cellules ou les poussières. L'exclusion des faux positifs ne doit pas être intégrée dans la couche logicielle de détection des cellules. Cela peut s'avérer difficile et représenter une perte de temps. Il faut accepter les faux positifs (un algorithme rudimentaire) et exclure manuellement les faux positifs à l'aide de notre oeil. Pour ne pas que cela devienne une corvée, on utilise la méthode du graphe de dispersion (scatter plot). Ce graphique "plot" simplement un paramètre en fonction d'un autre: par exemple l'aire en fonction du facteur de circularité (indication sur la forme des cellules). Cela "trie" les cellules et permet de séparer (et visualiser) les mauvais groupes d'objets détectés et les bons groupes. De simple fonctionnalités "user friendly" permettront de sélectionner (entourer) les bons objets pour ne travailler qu'avec eux dans la suite de l'analyse (c'est le concept de "gate" ). Pour résumer: Développeurs: ne perdez pas de temps à implémenter des fonctionnalités trop complexes dans le processus de détection d'objets. Préférez l'utilisation a posteriori des graphes de dispersion (figure 3). La video 2 illustre, en quelques minutes, la puissance de la cytométrie en image.
Le bruit intrinsèque et le bruit extrinsèque
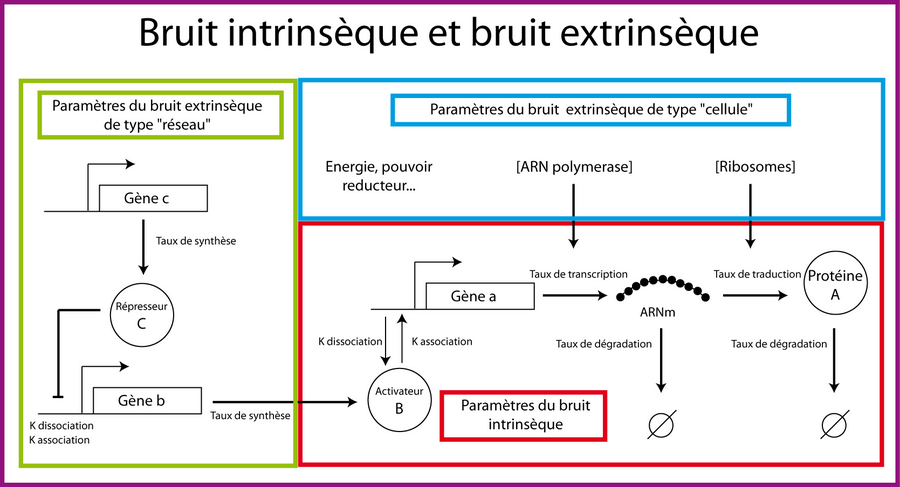
Il existe différentes sources de bruit qu'il convient de distinguer. Les variations d'expression génique inhérentes au processus biochimique de l'expression génique sont appelées bruit intrinsèque. On peut définir le bruit intrinsèque comme étant les fluctuations générées par l'activation et la désactivation stochastique d'un promoteur, ainsi que celles générées par la synthèse et la dégradation des ARNm et protéines (figure 4). Le bruit extrinsèque, lui, provient de deux sources:
- le bruit extrinsèque relatif au réseau. Ce bruit est généré par les fluctuations des concentrations des facteurs de transcription contrôlant l'expression d'un gène. Ainsi le bruit intrinsèque dans l'expression d'un gène a codant pour un facteur de transcription A représente aussi le bruit extrinsèque vis-à-vis de l'expression du gène b qui est activé par le facteur de transcription A.
- le bruit extrinsèque relatif à la cellule. Ce bruit provient des fluctuations dans les concentrations des ribosomes, de l'ARN polymérase, des métabolites, le volume de la cellule, l'état de la cellule dans le cycle cellulaire (car avant la division cellulaire, une cellule peut posséder plusieurs copies du même gène)...
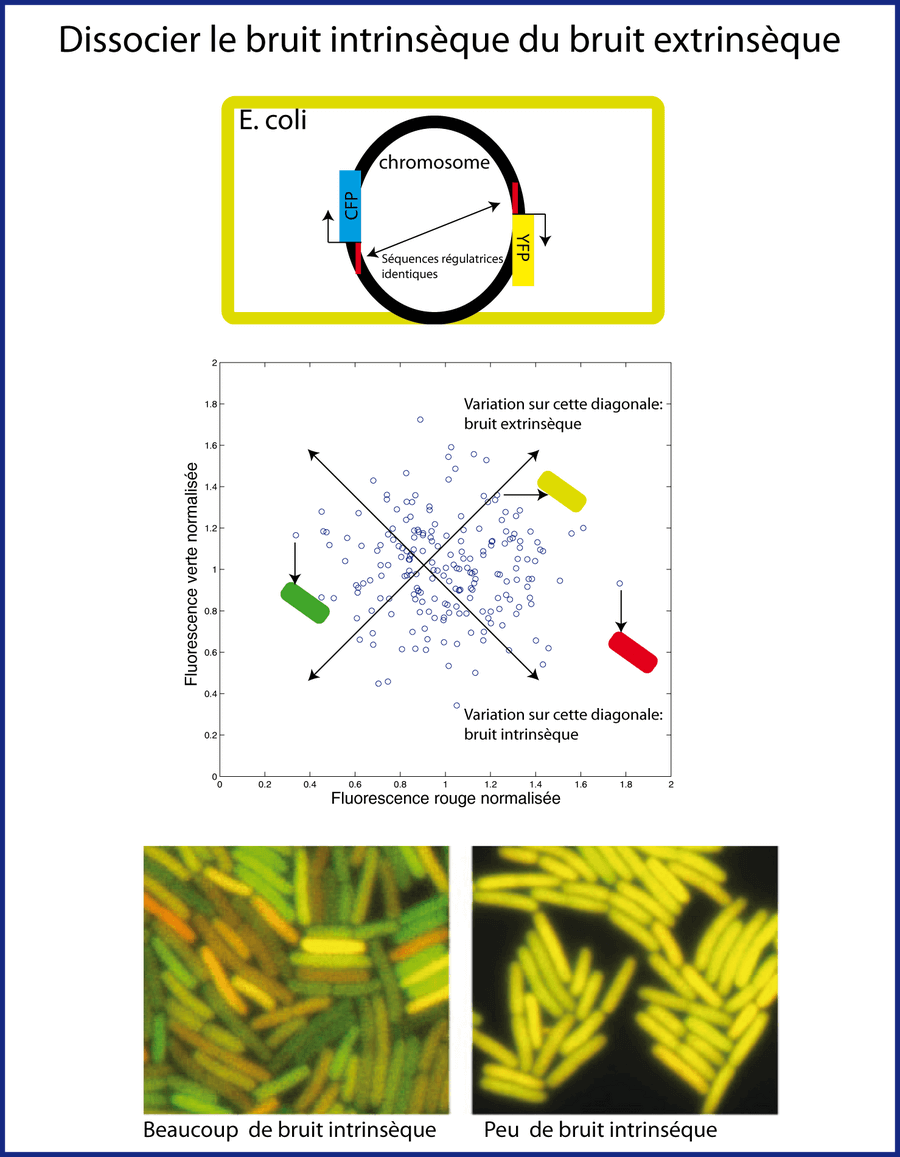
En 2002, l'équipe de Michael Elowitz à Caltech en Californie, a proposé une méthode permettant de distinguer le bruit intrinsèque du bruit extrinsèque (Elowitz et al. 2002). Cette méthode consiste à quantifier l'expression de deux gènes rapporteurs (YFP et CFP) placés à deux endroits équivalents sur le chromosome d'E. coli. Si l'expression des gènes était déterministe, toutes les cellules d'une population devrait avoir exactement la même concentration de protéine fluorescente jaune (YFP) et bleue (CFP): les cellules devraient toutes avoir la couleur verte. Ce n'est évidemment pas ce qu'ont observé les chercheurs: la couleur de fluorescence varie d'une bactérie à l'autre, allant du jaune à l'orange en passant par le vert. Le bruit intrinsèque est le bruit qui génère une différence de concentration de rapporteurs (YFP et CFP) dans la même cellule. Sur un graphe de dispersion représentant la fluorescence jaune en fonction de la fluorescence verte, le bruit intrinsèque peut être évalué sur la diagonale qui descend de gauche à droite. A l'inverse, le bruit extrinsèque est évalué sur la diagonale qui monte de gauche à droite (figure 5). Il représente les fluctuations des éléments (facteur de transcription, machinerie globale) qui affectent les concentrations de deux rapporteurs de manière identique dans une cellule donnée mais créent des différences entre deux cellules.
Les modèles stochastiques
Les équations maîtresses
Des connaissances plus poussées en mathématique deviennent nécessaires pour comprendre en détail les publications décrivant des modèles stochastiques de l'expression génique. La question de la modélisation du bruit en biologie semble d'ailleurs plutôt avoir été capturée par les physiciens et mathématiciens. Cependant, j'ai dans l'idée que nous, biologistes, pouvons tout de même réussir à comprendre les concepts, la substance pour pouvoir ne serait-ce que discuter avec un mathématicien. Je vais essayer de mettre en avant ce que je comprends et ce qui me semble important mais je demande une certaine indulgence à mon lecteur si perdurent quelques inepties. Dans ce cas, le lecteur pourrait directement consulter mes sources: des tutoriaux trouvés sur Internet (Biology of the noisy gene: Juan F. Poyatos ; Single cell experiments and Gillespie's algorithm: Fernand Hayot).
Pour expliquer comment on modélise l'expression stochastique des gènes, je vais repartir de l'équation la plus simple décrite dans le chapitre sur la modélisation.
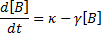
Notez que dans ce cas d'école extrêmement simple, il n'y a pas de régulation transcriptionnelle et on ne découple pas la production des ARNm et des protéines alors qu'il y a également introduction de bruit lors de ces étapes. Des modèles plus rigoureux mais un peu plus complexes découplant transcription et traduction existent également (Thattai and van Oudenaarden 2001).
Nous allons transformer cette équation de manière à ce qu'elle puisse décrire/intégrer les variations de la concentration de la protéine B dans une population de cellules. Le mot clé dont nous avons besoin est le mot probabilité. Pour cela, on utilise un type particulier d'équations différentielles dites équations maitresses (master equations). Une équation maîtresse est une équation différentielle décrivant l'évolution temporelle d'une distribution de probabilité. Cette distribution représente la probabilité d'un système d'occuper chacun des ensembles d'état discret (1, 2, 3 protéines par cellules...) en regard d'une variable de temps continue. Autrement dit, on va remplacer la concentration (c'est à dire la concentration moyenne de la protéine B dans la population de cellules) par une probabilité.
Si on raisonne à l'échelle de la cellule, on travaillera avec une probabilité P(n, t) d'avoir n protéines de type B dans une cellule à un temps t: par exemple, il y aura 25% de chance (0.25) d'avoir 3 protéines B dans la cellule, 50% de chance (0.5) d'avoir 4 protéines B dans la cellule et 25% de chance (0.25) d'avoir 5 protéines B dans la cellule.
Si on raisonne à l'échelle de la population (grand nombre de cellules), cette probabilité "se transforme" en distribution. En reprenant l'exemple précédent, si on a 1000 cellules: cela signifie qu'approximativement 250 cellules auront 3 protéines B, 500 cellules auront 4 protéines B et 250 cellules auront 5 protéines B.
On ne décrit plus l'évolution de la concentration moyenne de B dans la population en fonction du temps: on décrit l'évolution de la distribution du nombre de protéines B dans la population en fonction du temps.
Voyons maintenant comment s'écrit cette équation. Soit P(n,t) la probabilité d'avoir n protéines de type
B dans une cellule à un temps t. Nous souhaitons décrire l'évolution de P(n,t) en fonction du temps
c'est-à-dire 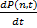 . Supposons qu'au temps t, l'état du
système soit connu, c'est à dire
le nombre de protéine B dans la cellule. Quelle est la probabilité P(n, t+dt) d'avoir n protéines B au
temps t+dt tel que dt soit suffisamment petit de manière à ce qu'une seule réaction de production ou
dégradation puisse se produire ? Il faut considérer trois possibilités (figure 6) :
. Supposons qu'au temps t, l'état du
système soit connu, c'est à dire
le nombre de protéine B dans la cellule. Quelle est la probabilité P(n, t+dt) d'avoir n protéines B au
temps t+dt tel que dt soit suffisamment petit de manière à ce qu'une seule réaction de production ou
dégradation puisse se produire ? Il faut considérer trois possibilités (figure 6) :
- Il y a n-1 protéines B au temps t et c'est l'événement de production qui a lieu au temps dt ce qui
donne une contribution à P(n,t+dt) égale à
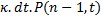
- Il y a n+1 protéines B au temps t et c'est l'événement de dégradation qui a lieu au temps dt ce qui
donne une contribution à P(n,t+dt) égale à
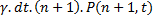 .
Pourquoi y a-t-il le facteur
(n+1) qui apparait ? A cause du fait que la vitesse de dégradation dépend du nombre de protéines
déjà présentes (voir le chapitre sur la modélisation)
.
Pourquoi y a-t-il le facteur
(n+1) qui apparait ? A cause du fait que la vitesse de dégradation dépend du nombre de protéines
déjà présentes (voir le chapitre sur la modélisation)
- Il n'y a aucune réaction qui se produit. Ce troisième point est un petit peu difficile à comprendre.
Les deux premiers points considèrent les probabilités "d'arriver" à n molécules soit
en venant de n-1 molécules (production) soit en venant de n+1 molécules (dégradation). Mais il faut
aussi prendre en considération la probabilité de ne pas "quitter/ bouger" de n
protéines durant le temps dt si on était déjà à n protéines au temps t. Cette probabilité c'est la
probabilité d'avoir n protéines au temps t, P(n,t) auquel on soustrait la probabilité qu'ait lieu un
événement de production
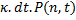 durant le temps dt ainsi
que la probabilité qu'ait lieu
un événement de dégradation
durant le temps dt ainsi
que la probabilité qu'ait lieu
un événement de dégradation 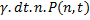 durant le temps dt.
durant le temps dt.

On a donc:
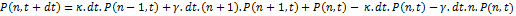
On peut ensuite passer sous forme de dérivée 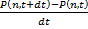 et on
obtient quasi
immédiatement l'équation ci-dessous qui correspond à l'équation maitresse:
et on
obtient quasi
immédiatement l'équation ci-dessous qui correspond à l'équation maitresse:
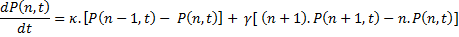
Retrouver l'équation déterministe à partir de l'équation maitresse
A partir de cette équation maitresse, on peut retrouver l'équation "déterministe" 3 des
concentrations 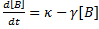 (La démonstration qui suit est un peu
fastidieuse: n'hésitez pas à la
sauter). Pour cela, il me faut introduire l'espérance
(La démonstration qui suit est un peu
fastidieuse: n'hésitez pas à la
sauter). Pour cela, il me faut introduire l'espérance
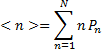
En prenant la dérivée par rapport au temps, on a:
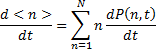
En remplaçant le terme de gauche par le résultat obtenu juste avant ce paragraphe, on obtient:
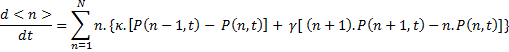
En remaniant et en se débarrassant des t encombrants, on obtient:
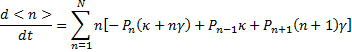
En sortant κ et γ des sommes, on obtient:
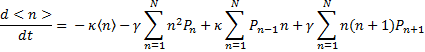
En factorisant κ et γ, on a:
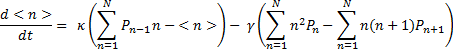
Focalisons-nous sur le premier terme (en considérant que n= n-1+1):
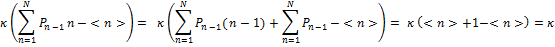
Puis focalisons-nous sur le deuxième terme (en considérant que n= n+1-1):
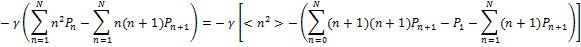
C'est-à-dire:
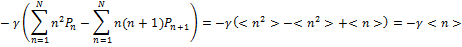
En reconstituant les deux termes, on retrouve bien:
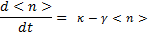
C'est-à-dire l'équivalent de notre équation déterministe initiale 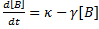
La loi de Poisson
A partir de l'équation 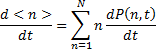 , on peut chercher les solutions
à l'état d'équilibre
c'est-à-dire quand
, on peut chercher les solutions
à l'état d'équilibre
c'est-à-dire quand 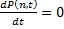 . Il existe une démonstration par récurrence
(trop difficile
pour moi ; voir le tutoriel de Fernand Hayot sur internet) qui montre que la distribution de P(n) suit
une loi de probabilité de la forme suivante:
. Il existe une démonstration par récurrence
(trop difficile
pour moi ; voir le tutoriel de Fernand Hayot sur internet) qui montre que la distribution de P(n) suit
une loi de probabilité de la forme suivante:
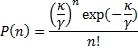
C'est à dire une loi de Poisson de la forme:
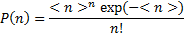
On repère bien que le terme  correspond à l'espérance
correspond à l'espérance 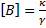 en résolvant l'équation
déterministe
en résolvant l'équation
déterministe 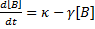 à l'état d'équilibre
à l'état d'équilibre 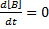 (voir le chapitre sur la modélisation). Ceci est donc encore un bon exemple montrant la
correspondance entre le comportement moyen du système déterministe et la moyenne (l'esperance) dans
la population obtenue avec la formulation stochastique.
(voir le chapitre sur la modélisation). Ceci est donc encore un bon exemple montrant la
correspondance entre le comportement moyen du système déterministe et la moyenne (l'esperance) dans
la population obtenue avec la formulation stochastique.
Mais que représente exactement ce bruit de Poisson ?
Nous avons vu qu'il est possible de mesurer l'expression génique (la fluorescence rapportant le nombre de molécules de GFP) de chaque cellule d'une population clonale placée dans un milieu identique. Les données obtenues permettent de "plotter"4 la distribution de fluorescence des cellules. Cette distribution de fluorescence reflète la distribution du nombre de protéines GFP dans les cellules. Une fois les distributions obtenues, on peut extraire des paramètres comme la moyenne ou la variance. De même, la forme de la distribution peut être comparée (fittée) avec de distributions connues comme les lois de gauss, gamma ou Poisson ce qui peut révéler les mécanismes sous jacent de la stochasticité. Dans notre cas, nous avons vu que le modèle stochastique le plus simple de l'expression d'un gène (pas de régulation, pas de passage par les ARN) suit une loi de poisson. C'est une loi discrète, adaptée à la description d'événements (nombre de molécules) rares. Une des caractéristiques de la loi de poisson c'est que la variance est égale à la moyenne. Notez que, au delà de 5 événements (molécules), la loi de poisson ressemble fortement à une loi normale dont la variance est égale à la moyenne.
Un paramètre qui est couramment utilisé pour évaluer la force du bruit est le facteur Fano F:
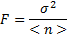
Dans notre cas d'école très simple de l'expression génique, la distribution des protéines suit une loi de Poisson donc F=1 car, je le répète, la variance est égale à la moyenne. Mais quand on travaille sur un système plus complexe intégrant des régulations géniques ou des boucles de rétroaction, les équations maitresses deviennent très complexes. La mesure du facteur Fano permet d'évaluer les déviations par rapport au comportement de Poisson (par rapport à 1).
L'algorithme de Gillespie
Lorsque le système devient trop complexe (la plupart du temps), les équations maitresses ne peuvent plus être intégrées analytiquement. On utilise, tout comme pour les équations déterministes, un algorithme numérique nommé algorithme de Gillespie. Notez cependant que contrairement aux méthodes d'approximation numérique utilisées par Matlab dans le chapitre de modélisation (Méthode de Runge-Kutta ; fonction de type ode45), l'algorithme de Gillespie est un algorithme exact: il n'introduit aucune erreur dans le processus itératif (Gillespie 1977). La description qui suit peut être utile à une personne cherchant à comprendre le fonctionnement de l'algorithme de Gillespie (script Matlab joint). Ceux qui ne souhaitent pas rentrer dans les détails peuvent sauter ce paragraphe.
Le point essentiel de cet algorithme consiste à créer deux nombre aléatoires: le premier sert à déterminer après combien de temps la prochaine réaction prendra place, le second permet de choisir quelle réaction chimique se produit. Dans notre exemple, il n'y a que deux réactions chimiques: synthèse et dégradation d'une protéine.
Supposons qu'il y ait μ=1,2,... réactions. aμ(t) est le produit de deux parties: la vitesse (le taux) de réaction cμ(t) et le nombre de réactions (collisions) possibles. Si par exemple on a:
Où Z est l'heterodimère formé par P1 et P2, on a:
aμ(t)= cμP1P2
où P1 et P2 représentent le nombre respectif de molécules de type P1 et P2. Le produit P1P2 représente donc bien le nombre de collisions possibles.
Voyons maintenant comment cet algorithme fonctionne. N'hésitez pas à jongler entre cette explication et le script Matlab qui reprend l'exemple simple de l'évolution d'une protéine P soumise à synthèse et dégradation dans une cellule.
Supposons que le système soit connu au temps t, ce qui signifie que le nombre de molécules de chaque type
est connu (ainsi que les taux de réactions). Par conséquent, la quantité aμ(t) est
connue pour
chaque réaction. aμ(t)dt est la probabilité que, étant donné l'état du système au
temps t, la
réaction μ se produise dans l'intervalle de temps (t,t+dt). Appelons 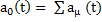 la somme
de tous les aμ(t). Le terme a0(t) dt est la probabilité que n'importe
quelle réaction se
produise durant le temps (t,t+dt).
la somme
de tous les aμ(t). Le terme a0(t) dt est la probabilité que n'importe
quelle réaction se
produise durant le temps (t,t+dt).
A partir de là, l'algorithme suit les étapes suivantes:
- On détermine le temps τ (après t) correspondant au temps où aura lieu la prochaine réaction. On crée un nombre aléatoire r1 à partir d'une distribution uniforme compris entre 0 et 1 puis on choisit τ selon l'équation suivante
- On choisit aléatoirement la réaction qui se produit au temps τ (dans notre cas soit la synthèse soit la dégradation). On crée un nombre aléatoire r2 à partir d'une distribution uniforme compris entre 0 et 1. Si ce nombre tombe entre 0 et a1/a0 la réaction 1 est choisie. Si il tombe entre a1/a0 et (a1+a2)/(a0), la réaction 2 est choisie et ainsi de suite.
- Le choix de la réaction a pour conséquence de changer le nombre de molécules au temps (t+τ). Dans notre cas, soit il y a synthèse soit il y a dégradation d'une protéine c'est-à-dire soit P -> P + 1 soit P -> P - 1 avec P le nombre de protéines. Ainsi la valeur d'aμ change. L'algorithme revient au point numéro 1 via une boucle "while" et le processus est réitéré "tant que" le temps maximum définit par l'utilisateur n'est pas atteint.
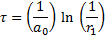
Cette équation est une fonction de densité de probabilité exponentielle. Elle est liée au fait que la probabilité qu'une réaction ait lieu croit de manière exponentielle lorsque le temps passe.
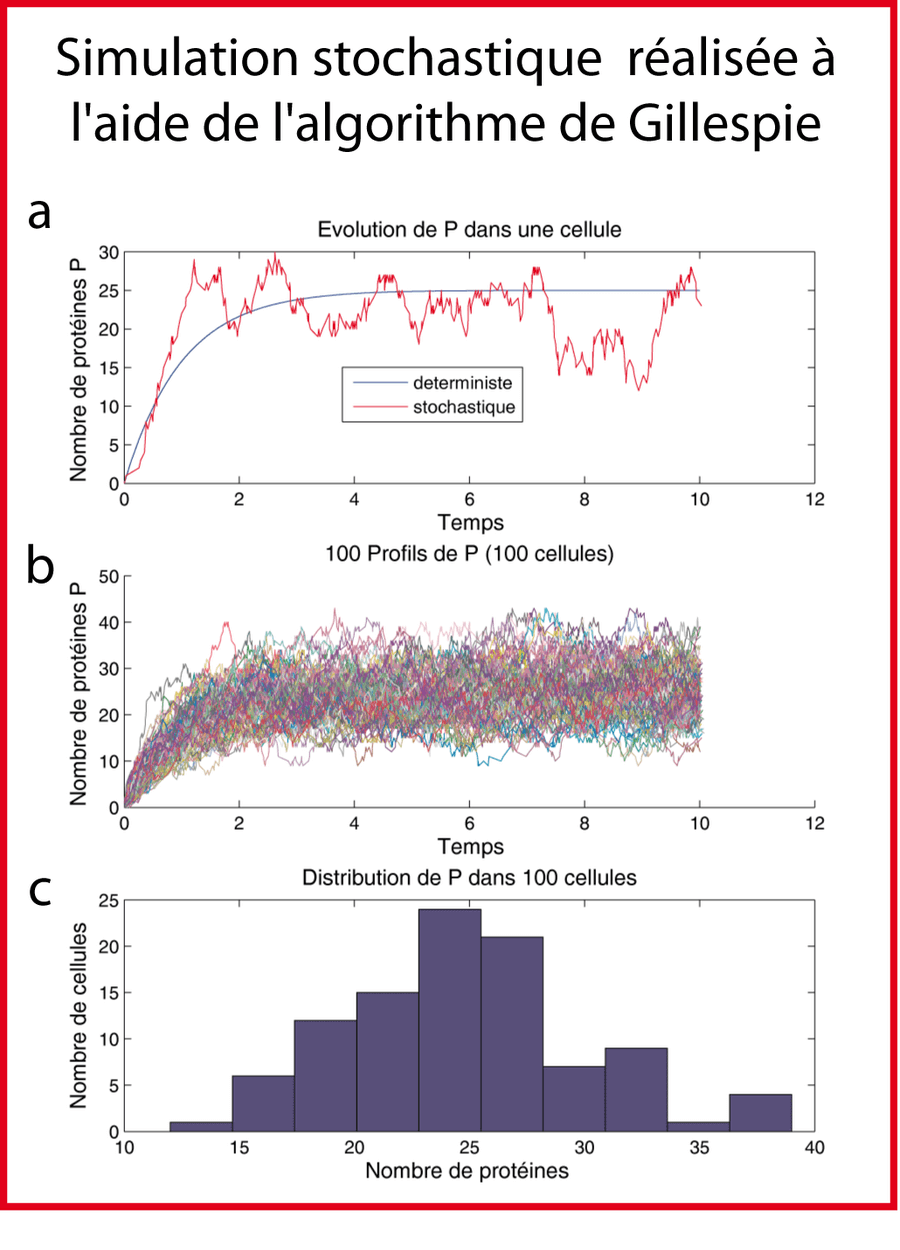
Dans notre cas d'école simple, on peut "plotter" , une fois la boucle "while" terminée, l'évolution du nombre de protéines P en fonction du temps et comparer le résultat avec la version déterministe (figure 8a). Mais on peut aussi placer une boucle for en amont de la boucle while: cette boucle for génère un profil (évolution de P en fonction du temps) différent à chaque itération c'est-à-dire pour chaque cellule ce qui nous permet de "plotter" les profils de 100 cellules par exemple (figure 8b). Si on extrait le nombre de molécules P atteint à la fin de chaque cinétique, on peut "plotter" la distribution de protéines P dans la population de cellules (figure 8c). Vous pourriez vouloir comparer (fitter) cette distribution avec la distribution obtenue expérimentalement dans le but d'identifier des paramètres ou dans le but de valider ou infirmer votre modèle.
Cliquer pour voir le code Matlab
function GillespieAlgorithm
% Algorithme de gillespie pour un petit modèle simple. ce script se base
% sur des versions de script de van Oudenaarden et Poyatos. Il est
% cependant largement modifié.
% une protéine P est synthétisé à un taux kappa et degradé à un taux gamma
clear all
figure('Color', 'w')
hold on
% cette boucle for reproduit l'algorithme de Gillespie 100 fois
% pour voir un grand de profils de cellules.
for NombreCellule=1:100
k= 25;% taux de synthèse
gamma = 1;% taux de dégradation
P = 0;% nombre de protèines
Tspan{NombreCellule}=[];
Pstochastic{NombreCellule} = P;% evolution de P au cours du temps
tmax = 10;% temps maximum
t = 0;%
tspan = t;
% debut de l'algorithme de Gillespie
while t < tmax
a = [k, gamma*P(1)];
a0 = sum(a);
% determine le temps de la prochaine reaction
r1 = rand;
tau = -log(r1)/a0;
t = t + tau;
% determine le type de reaction
r2 = rand;
acumsum = cumsum(a)/a0;
chosen_reaction = min(find(r2 <= acumsum));
if chosen_reaction == 1;
P(1) = P(1) + 1; %evenement de synthèse
else
P(1) = P(1) - 1;%evenement de degradation
end
tspan = [tspan,t];
Tspan{NombreCellule}=tspan;% stoc les temps
% stoc l'evolution de P dans Pstochastic
Pstochastic{NombreCellule} = [Pstochastic{NombreCellule};P];
end
% Stoc la valeur finale de P à la fin de chaque cinétique
Distribution(NombreCellule)= Pstochastic{NombreCellule}(end)
end
% equatiion deterministe
P0 = 0;
options = [];
[t P] = ode23(@code1equations,tspan,P0,options,k,gamma);
% plot de la concentration de P en fonction du temps avec les deux modèles
handle1=subplot(3,1,1)
plot(t,P,Tspan{1},Pstochastic{1},'r')
legend('deterministe','stochastique')
xlabel('Temps','Fontsize',12)
ylabel('Nombre de protéines P','Fontsize',12)
title ('Evolution de P dans une cellule','Fontsize',12)
% plot de 100 profils (100 cellules)
handle2=subplot(3,1,2)
hold(handle2)
for i=1:NombreCellule
plot(Tspan{i},Pstochastic{i},'color',[rand rand rand])
end
xlabel('Temps','Fontsize',12)
ylabel('Nombre de protéines P','Fontsize',12)
title ('100 Profils de P (100 cellules)','Fontsize',12)
% histogramme de la distribution de P dans les 100 cellules.
handle3=subplot(3,1,3)
hist(Distribution)
xlabel('Nombre de protéines','Fontsize',12)
ylabel('Nombre de cellules','Fontsize',12)
title ('Distribution de P dans 100 cellules','Fontsize',12)
function dPdt = code1equations(t,P,kappa,gamma)
dPdt = [kappa-gamma*P(1)];
end
end
Modèle spatial didactique
Avant de commencer mon master 2, je pensais que les scientifiques réussiraient sans doute rapidement (décennies) à créer une cellule virtuelle in silico (de Jong and Rechenmann 2005). Intéressé par ce type de recherche, j'ai rencontré [2023 : identité protégée] et commencé à travailler sur la modélisation des réseaux de régulation génique sous sa direction. A posteriori, je me rends compte maintenant de ma naïveté cachée derrière l'idée de créer une cellule virtuelle.
Cliquer pour voir le code Matlab
%% E.Coli virtuelle
% Cette bacterie virtuelle a été crée pour augmenter l'experience matlab:
% l'objectif était de faire generer des oscillations basées sur la pulbi de
% elowitz à l'aide du mouvement brownien, le tout visualisable en 3D.
% pour fabriquer le film, decommenter le code film
%% petit necessité de visualisation
function Oscillation3D
F=figure;
set(F,'color','w')
graph2D =axes('Fontsize', 18,'Units','pixels', 'Position',...
[100 500-450 400 100]);
axis([0 2000 0 100]);
graph3D =axes( 'Fontsize', 8,'Units','pixels', 'Position',...
[100 500-330 400 300]);
axis([-1.3 1.8 -1.0 1 -1 1]);
axis off
set([graph2D,graph3D],'Units','normalized')
hold on
grid off
box off
xlabel(graph2D,'Time (minutes)','fontsize',18)
ylabel(graph2D,'Proteins/cell','fontsize',18)
%code film
%mov=avifile('testfilmavrilN11.avi','compression','Cinepak','quality',100);
%% definition des paramètres
temps=2000; % temps
n=1;% nombre de proteine A
m=1;% nombre proteine B
q=1;% nombre de protéine C
vitesse=0.06; % vitesse des molécules dans la bacterie
v1=vitesse*ones(n,1);% vitesse
v2=vitesse*ones(m,1);% vitesse
v3=vitesse*ones(q,1);% vitesse
KappaA=100; % taux de synthèse
KappaB=100;% taux de synthèse
KappaC=100;% taux de synthèse
KappaA_init=100; % taux de synthèse
KappaB_init=100;% taux de synthèse
KappaC_init=100;% taux de synthèse
GammaA=1;% taux de dégradation
GammaB=1; % taux de dégradation
GammaC=1;% taux de dégradation
kaffAsurb=1.98;% compris entre 1 et 2
kaffBsurc=1.98;% compris entre 1 et 2
kaffCsura=1.98;% compris entre 1 et 2
SyntheseA=0; %alloue de l'espace
DegradationA=0; %alloue de l'espace
SyntheseB=0; %alloue de l'espace
DegradationB=0; %alloue de l'espace
SyntheseC=0; %alloue de l'espace
DegradationC=0; %alloue de l'espace
N=[];% ensemble des valeurs de N
M=[];
Q=[];
I=[];
xc=0;% sert à générer l'ellipsoid (forme coli)
yc=0;
zc=0;
xr=2;
yr=1;
zr=1;
mt=20;
% génére alleatoirement les coordonées de départ des molcules
A=(rand(n,1)-0.5)*2; % nombre aléatoire entre -1 et 1 (je crois)
% voir equation ellipsoide
A=[A(:,1) sqrt(yr.^2*((1-A(:,1).^2/xr.^2))).*(rand(n,1)-0.5)*2 ];
A=[A(:,1) A(:,2) sqrt(zr.^2*((1-(A(:,1).^2/xr.^2)-(A(:,2).^2/yr.^2))))....
*(rand(n,1)-0.5)*2 zeros(n,1) zeros(n,1) zeros(n,1)];
B=(rand(m,1)-0.5)*2;
B=[B(:,1) sqrt(yr.^2*((1-B(:,1).^2/xr.^2))).*(rand(m,1)-0.5)*2 ];
B=[B(:,1) B(:,2) sqrt(zr.^2*((1-(B(:,1).^2/xr.^2)-(B(:,2).^2/yr.^2))))....
*(rand(m,1)-0.5)*2 zeros(m,1) zeros(m,1) zeros(m,1)];
C=(rand(q,1)-0.5)*2;
C=[C(:,1) sqrt(yr.^2*((1-C(:,1).^2/xr.^2))).*(rand(q,1)-0.5)*2 ];
C=[C(:,1) C(:,2) sqrt(zr.^2*((1-(C(:,1).^2/xr.^2)-(C(:,2).^2/yr.^2))))....
*(rand(q,1)-0.5)*2 zeros(q,1) zeros(q,1) zeros(q,1)];
%% simple hélice d'ADN
t=0:pi/50000:2*pi;% nombre de point de l'hélice d'ADN
% plot3((cos(t*1000)/150)+cos(t), sin(t*1000)/150,sin(t),'color','r');%
% plot l'hélice d'ADN mais sans le double superenroulement
plot3((cos(t*100)/50)+cos(t), sin(t*100)/50+cos(t*5000)/500,...
sin(t)+sin(t*5000)/500,'color','r');
% definit les zones ou seront plotées les bases atcg
promoteurA=0.33*pi:pi/500:0.53*pi;
% affiche sequence codante
text((cos(promoteurA*100)/50)+cos(promoteurA),sin(promoteurA*100)...
/50+cos(promoteurA*5000)/500,sin(promoteurA)+sin(promoteurA*5000)...
/500,randsample('ATCG',101,true,[0.5 0.5 0.5 0.5])','Color','r');
promoteurB=1.00*pi:pi/500:1.20*pi;
% affiche sequence codante
text((cos(promoteurB*100)/50)+cos(promoteurB),sin(promoteurB*100)...
/50+cos(promoteurB*5000)/500,sin(promoteurB)+sin(promoteurB*5000)...
/500,randsample('ATCG',101,true,[0.5 0.5 0.5 0.5])','Color','g');
promoteurC=1.66*pi:pi/500:1.86*pi;
% affiche sequence codante
text((cos(promoteurC*100)/50)+cos(promoteurC),sin(promoteurC*100)...
/50+cos(promoteurC*5000)/500,sin(promoteurC)+sin(promoteurC*5000)...
/500,randsample('ATCG',101,true,[0.5 0.5 0.5 0.5])','Color','b');
%% membrane coli
[x, y, z] = ellipsoid(xc,yc,zc,xr,yr,zr,mt);
surface(x, y, z,'EdgeColor','y','FaceColor','y')
alpha(0.1)%transparence
%% fabrication des cubes
for chaqueN=1:n % boucle de la protéine cubique A
vert1 = [A(chaqueN,1) A(chaqueN,2) A(chaqueN,3);...
A(chaqueN,1) A(chaqueN,2)+0.02 A(chaqueN,3);...
A(chaqueN,1)+0.02 A(chaqueN,2)+0.02 A(chaqueN,3);...
A(chaqueN,1)+0.02 A(chaqueN,2) A(chaqueN,3) ; ...
A(chaqueN,1) A(chaqueN,2) A(chaqueN,3)+0.02;...
A(chaqueN,1) A(chaqueN,2)+0.02 A(chaqueN,3)+0.02;...
A(chaqueN,1)+0.02 A(chaqueN,2)+0.02 A(chaqueN,3)+0.02;...
A(chaqueN,1)+0.02 A(chaqueN,2)...
A(chaqueN,3)+0.02];
fac = [1 2 3 4; ...
2 6 7 3; ...
4 3 7 8; ...
1 5 8 4; ...
1 2 6 5; ...
5 6 7 8];
graph1(chaqueN)=patch('Faces',fac,'Vertices',vert1,'FaceColor','r');
chaqueN=chaqueN+1;
end
for chaqueM=1:m % boucle de la protéine cubique B
vert2 = [B(chaqueM,1) B(chaqueM,2) B(chaqueM,3);...
B(chaqueM,1) B(chaqueM,2)+0.02 B(chaqueM,3);...
B(chaqueM,1)+0.02 B(chaqueM,2)+0.02 B(chaqueM,3);...
B(chaqueM,1)+0.02 B(chaqueM,2) B(chaqueM,3) ; ...
B(chaqueM,1) B(chaqueM,2) B(chaqueM,3)+0.02;...
B(chaqueM,1) B(chaqueM,2)+0.02 B(chaqueM,3)+0.02;...
B(chaqueM,1)+0.02 B(chaqueM,2)+0.02 B(chaqueM,3)+0.02;...
B(chaqueM,1)+0.02 B(chaqueM,2)...
B(chaqueM,3)+0.02];
fac = [1 2 3 4; ...
2 6 7 3; ...
4 3 7 8; ...
1 5 8 4; ...
1 2 6 5; ...
5 6 7 8];
graph2(chaqueM)=patch('Faces',fac,'Vertices',vert2,'FaceColor','g');
chaqueM=chaqueM+1;
end
for chaqueQ=1:q % boucle de la protéine cubique C
vert3 = [C(chaqueQ,1) C(chaqueQ,2) C(chaqueQ,3);...
C(chaqueQ,1) C(chaqueQ,2)+0.02 C(chaqueQ,3);...
C(chaqueQ,1)+0.02 C(chaqueQ,2)+0.02 C(chaqueQ,3);...
C(chaqueQ,1)+0.02 C(chaqueQ,2) C(chaqueQ,3) ; ...
C(chaqueQ,1) C(chaqueQ,2) C(chaqueQ,3)+0.02;...
C(chaqueQ,1) C(chaqueQ,2)+0.02 C(chaqueQ,3)+0.02;...
C(chaqueQ,1)+0.02 C(chaqueQ,2)+0.02 C(chaqueQ,3)+0.02;...
C(chaqueQ,1)+0.02 C(chaqueQ,2)...
C(chaqueQ,3)+0.02];
fac = [1 2 3 4; ...
2 6 7 3; ...
4 3 7 8; ...
1 5 8 4; ...
1 2 6 5; ...
5 6 7 8];
graph3(chaqueQ)=patch('Faces',fac,'Vertices',vert3,'FaceColor','b');
chaqueQ=chaqueQ+1;
end
%% creation de la vie bacterienne !!
for i=1:temps % definit le temps
A(:,4)=(rand(n,1)-0.5)*2;% choisit une variation aléatoire sur x
A(:,5)=(rand(n,1)-0.5)*2;% choisit une variation aléatoire sur y
A(:,6)=(rand(n,1)-0.5)*2;% choisit une variation aléatoire sur z
A(:,1)=A(:,1)+v1(:,1).*A(:,4);% equation du mouvement brownien
A(:,2)=A(:,2)+v1(:,1).*A(:,5);
A(:,3)=A(:,3)+v1(:,1).*A(:,6);
B(:,4)=(rand(m,1)-0.5)*2;
B(:,5)=(rand(m,1)-0.5)*2;
B(:,6)=(rand(m,1)-0.5)*2;
B(:,1)=B(:,1)+v2(:,1).*B(:,4);
B(:,2)=B(:,2)+v2(:,1).*B(:,5);
B(:,3)=B(:,3)+v2(:,1).*B(:,6);
C(:,4)=(rand(q,1)-0.5)*2;
C(:,5)=(rand(q,1)-0.5)*2;
C(:,6)=(rand(q,1)-0.5)*2;
C(:,1)=C(:,1)+v3(:,1).*C(:,4);
C(:,2)=C(:,2)+v3(:,1).*C(:,5);
C(:,3)=C(:,3)+v3(:,1).*C(:,6);
%% rester dans le cocon familial elipsoidal
chaqueN=1;
for chaqueN=1:n
if (A(chaqueN,1)-xc).^2/xr.^2+(A(chaqueN,2)-yc).^2/yr.^2+...
(A(chaqueN,3)-zc).^2/zr.^2>1 % voir equation ellipsoid
A(chaqueN,:)=[A(chaqueN,1)-v1(chaqueN,1)...
*A(chaqueN,4) A(chaqueN,2)-v1(chaqueN,1)...
*A(chaqueN,5) A(chaqueN,3)-v1(chaqueN,1)*A(chaqueN,6) 0 0 0];
end
chaqueN=chaqueN+1;
end
chaqueM=1;
for chaqueM=1:m
if (B(chaqueM,1)-xc).^2/xr.^2+(B(chaqueM,2)-yc).^2/yr.^2+...
(B(chaqueM,3)-zc).^2/zr.^2>1
B(chaqueM,:)=[B(chaqueM,1)-v2(chaqueM,1)...
*B(chaqueM,4) B(chaqueM,2)-v2(chaqueM,1)...
*B(chaqueM,5) B(chaqueM,3)-v2(chaqueM,1)*B(chaqueM,6) 0 0 0];
end
chaqueM=chaqueM+1;
end
chaqueQ=1;
for chaqueQ=1:q
if (C(chaqueQ,1)-xc).^2/xr.^2+(C(chaqueQ,2)-yc).^2/yr.^2+...
(C(chaqueQ,3)-zc).^2/zr.^2>1
C(chaqueQ,:)=[C(chaqueQ,1)-v3(chaqueQ,1)...
*C(chaqueQ,4) C(chaqueQ,2)-v3(chaqueQ,1)...
*C(chaqueQ,5) C(chaqueQ,3)-v3(chaqueQ,1)*C(chaqueQ,6) 0 0 0];
end
chaqueQ=chaqueQ+1;
end
%% synthese et degradatation
SyntheseA=SyntheseA+KappaA;
if SyntheseA>100 % definit la manière dont se passe la synthèse
n=n+1;
% cree une nouvelle protéine à l'interieur de l'ellipsoid
A(n,1)=(rand(1)-0.5)*2;
A(n,2)=sqrt(yr.^2*((1-A(n,1).^2/xr.^2))).*(rand(1)-0.5)*2 ;
A(n,:)=[A(n,1) A(n,2) sqrt(zr.^2*((1-(A(n,1).^2/xr.^2)-...
(A(n,2).^2/yr.^2)))).*(rand(1)-0.5)*2 0 0 0];
vert1 = [A(n,1) A(n,2) A(n,3); A(n,1) A(n,2)+0.02 A(n,3);...
A(n,1)+0.02 A(n,2)+0.02 A(n,3); A(n,1)+0.02 A(n,2) A(n,3) ; ...
A(n,1) A(n,2) A(n,3)+0.02;A(n,1) A(n,2)+0.02 A(n,3)+0.02;...
A(n,1)+0.02 A(n,2)+0.02 A(n,3)+0.02;A(n,1)+0.02 A(n,2)...
A(n,3)+0.02];
graph1(n)=patch('Faces',fac,'Vertices',vert1,'FaceColor','r');
SyntheseA=0;
v1=[v1; vitesse] ;
end
% equation correcte pour la degradation
DegradationA=DegradationA+GammaA*n;
if DegradationA>100 % definit la manière dont se passe la dégradation
if v1(n,:)==0
KappaB=KappaB_init;
v1(n,:)=[];
A(n,:)=[];
delete (graph1(n))
n=n-1;
DegradationA=0;
else
v1(n,:)=[];
A(n,:)=[];
delete (graph1(n))
n=n-1;
DegradationA=0;
end
end
SyntheseB=SyntheseB+KappaB;
if SyntheseB>100 % definit la manière dont se passe la synthèse
m=m+1;
B(m,1)=(rand(1)-0.5)*2;
B(m,2)=sqrt(yr.^2*((1-B(m,1).^2/xr.^2))).*(rand(1)-0.5)*2 ;
B(m,:)=[B(m,1) B(m,2) sqrt(zr.^2*((1-(B(m,1).^2/xr.^2)-...
(B(m,2).^2/yr.^2)))).*(rand(1)-0.5)*2 0 0 0];
vert2 = [B(m,1) B(m,2) B(m,3); B(m,1) B(m,2)+0.02 B(m,3);...
B(m,1)+0.02 B(m,2)+0.02 B(m,3); B(m,1)+0.02 B(m,2) B(m,3) ; ...
B(m,1) B(m,2) B(m,3)+0.02;B(m,1) B(m,2)+0.02 B(m,3)+0.02;...
B(m,1)+0.02 B(m,2)+0.02 B(m,3)+0.02;B(m,1)+0.02 B(m,2)...
B(m,3)+0.02];
graph2(m)=patch('Faces',fac,'Vertices',vert2,'FaceColor','g');
SyntheseB=0;
v2=[v2; vitesse] ;
end
DegradationB=DegradationB+GammaB*m;
if DegradationB>100 % definit la manière dont se passe la dégradation
if v2(m,:)==0
KappaC=KappaC_init;
v2(m,:)=[];
B(m,:)=[];
delete (graph2(m))
m=m-1;
DegradationB=0;
else
v2(m,:)=[];
B(m,:)=[];
delete (graph2(m))
m=m-1;
DegradationB=0;
end
end
SyntheseC=SyntheseC+KappaC;
if SyntheseC>100 % definit la manière dont se passe la synthèse
q=q+1;
C(q,1)=(rand(1)-0.5)*2;
C(q,2)=sqrt(yr.^2*((1-C(q,1).^2/xr.^2))).*(rand(1)-0.5)*2 ;
C(q,:)=[C(q,1) C(q,2) sqrt(zr.^2*((1-(C(q,1).^2/xr.^2)...
-(C(q,2).^2/yr.^2)))).*(rand(1)-0.5)*2 0 0 0];
vert3 = [C(q,1) C(q,2) C(q,3); C(q,1) C(q,2)+0.02 C(q,3);...
C(q,1)+0.02 C(q,2)+0.02 C(q,3); C(q,1)+0.02 C(q,2) C(q,3) ; ...
C(q,1) C(q,2) C(q,3)+0.02;C(q,1) C(q,2)+0.02 C(q,3)+0.02;...
C(q,1)+0.02 C(q,2)+0.02 C(q,3)+0.02;C(q,1)+0.02 C(q,2)...
C(q,3)+0.02];
graph3(q)=patch('Faces',fac,'Vertices',vert3,'FaceColor','b');
SyntheseC=0;
v3=[v3; vitesse] ;
end
DegradationC=DegradationC+GammaC*q;
if DegradationC>100 % definit la manière dont se passe la dégradation
if v3(q,:)==0
KappaA=KappaA_init;
v3(q,:)=[];
C(q,:)=[];
delete (graph3(q))
q=q-1;
DegradationC=0;
else
v3(q,:)=[];
C(q,:)=[];
delete (graph3(q))
q=q-1;
DegradationC=0;
end
end
%% fixation à son promoteur préféré: cette fixation n'est pas parfaite
chaqueN=1;
for chaqueN=1:n
if A(chaqueN,1)cos(pi*1000)/150+cos(pi)-0.2 &&...
A(chaqueN,2)sin(pi*1000)/150-0.2 &&...
A(chaqueN,3)sin(pi)-0.2 ;
v1(chaqueN,1)=0;
KappaB=GammaB;
LienAsurb=rand(1)/kaffAsurb;
if LienAsurb>0.5
v1(chaqueN,1)=vitesse;
KappaB=KappaB_init;
end
end
chaqueN=chaqueN+1;
end
chaqueM=1 ;
for chaqueM=1:m
if B(chaqueM,1)cos(1.66*pi*1000)/150+cos(1.66*pi)-0.2 &&...
B(chaqueM,2)sin(1.66*pi*1000)/150-0.2 &&...
B(chaqueM,3)sin(1.66*pi)-0.2 ;
v2(chaqueM,1)=0;
KappaC=GammaC;
LienBsurc=rand(1)/kaffBsurc;
if LienBsurc>0.5
v2(chaqueM,1)=vitesse;
KappaC=KappaC_init;
end
end
chaqueM=chaqueM+1;
end
chaqueQ=1 ;
for chaqueQ=1:q
if C(chaqueQ,1)cos(0.33*pi*1000)/150+cos(0.33*pi)-0.2 &&...
C(chaqueQ,2)sin(0.33*pi*1000)/150-0.2 &&...
C(chaqueQ,3)sin(0.33*pi)-0.2 ;
v3(chaqueQ,1)=0;
KappaA=GammaA;
LienCsura=rand(1)/kaffCsura;
if LienCsura>0.5
v3(chaqueQ,1)=vitesse;
KappaA=KappaA_init;
end
end
chaqueQ=chaqueQ+1;
end
%% visualisation à chaque itération
chaqueN=1;
for chaqueN=1:n
set(graph1(chaqueN),'XData',[A(chaqueN,1) A(chaqueN,1) ...
A(chaqueN,1)+0.02 A(chaqueN,1) A(chaqueN,1) A(chaqueN,1);...
A(chaqueN,1) A(chaqueN,1) A(chaqueN,1)+0.02 A(chaqueN,1)...
A(chaqueN,1) A(chaqueN,1) ;...
A(chaqueN,1)+0.02 A(chaqueN,1)+0.02...
A(chaqueN,1)+0.02 A(chaqueN,1)+0.02...
A(chaqueN,1) A(chaqueN,1)+0.02 ;...
A(chaqueN,1)+0.02 A(chaqueN,1)+0.02...
A(chaqueN,1)+0.02 A(chaqueN,1)+0.02...
A(chaqueN,1) A(chaqueN,1)+0.02],...
'YData',[A(chaqueN,2) A(chaqueN,2)+0.02...
A(chaqueN,2) A(chaqueN,2) A(chaqueN,2) A(chaqueN,2) ;...
A(chaqueN,2)+0.02 A(chaqueN,2)+0.02...
A(chaqueN,2)+0.02 A(chaqueN,2) A(chaqueN,2)+0.02...
A(chaqueN,2)+0.02 ;...
A(chaqueN,2)+0.02 A(chaqueN,2)+0.02 A(chaqueN,2)+0.02...
A(chaqueN,2) A(chaqueN,2)+0.02 A(chaqueN,2)+0.02;...
A(chaqueN,2) A(chaqueN,2)+0.02...
A(chaqueN,2) A(chaqueN,2) A(chaqueN,2) A(chaqueN,2)],...
'ZData',[A(chaqueN,3) A(chaqueN,3) A(chaqueN,3)...
A(chaqueN,3) A(chaqueN,3) A(chaqueN,3)+0.02 ;...
A(chaqueN,3) A(chaqueN,3)+0.02...
A(chaqueN,3) A(chaqueN,3)+0.02 A(chaqueN,3) A(chaqueN,3)+0.02 ;...
A(chaqueN,3) A(chaqueN,3)+0.02...
A(chaqueN,3)+0.02 A(chaqueN,3)+0.02...
A(chaqueN,3)+0.02 A(chaqueN,3)+0.02;...
A(chaqueN,3) A(chaqueN,3) A(chaqueN,3)+0.02...
A(chaqueN,3) A(chaqueN,3)+0.02 A(chaqueN,3)+0.02])
chaqueN=chaqueN+1;
end
for chaqueM=1:m
set(graph2(chaqueM),'XData',[B(chaqueM,1) B(chaqueM,1) ...
B(chaqueM,1)+0.02 B(chaqueM,1) B(chaqueM,1) B(chaqueM,1);...
B(chaqueM,1) B(chaqueM,1) B(chaqueM,1)+0.02 B(chaqueM,1)...
B(chaqueM,1) B(chaqueM,1) ;...
B(chaqueM,1)+0.02 B(chaqueM,1)+0.02...
B(chaqueM,1)+0.02 B(chaqueM,1)+0.02...
B(chaqueM,1) B(chaqueM,1)+0.02 ;...
B(chaqueM,1)+0.02 B(chaqueM,1)+0.02...
B(chaqueM,1)+0.02 B(chaqueM,1)+0.02...
B(chaqueM,1) B(chaqueM,1)+0.02],...
'YData',[B(chaqueM,2) B(chaqueM,2)+0.02...
B(chaqueM,2) B(chaqueM,2) B(chaqueM,2) B(chaqueM,2) ;...
B(chaqueM,2)+0.02 B(chaqueM,2)+0.02...
B(chaqueM,2)+0.02 B(chaqueM,2) B(chaqueM,2)+0.02...
B(chaqueM,2)+0.02 ;...
B(chaqueM,2)+0.02 B(chaqueM,2)+0.02 B(chaqueM,2)+0.02...
B(chaqueM,2) B(chaqueM,2)+0.02 B(chaqueM,2)+0.02;...
B(chaqueM,2) B(chaqueM,2)+0.02...
B(chaqueM,2) B(chaqueM,2) B(chaqueM,2) B(chaqueM,2)],...
'ZData',[B(chaqueM,3) B(chaqueM,3) B(chaqueM,3)...
B(chaqueM,3) B(chaqueM,3) B(chaqueM,3)+0.02 ;...
B(chaqueM,3) B(chaqueM,3)+0.02...
B(chaqueM,3) B(chaqueM,3)+0.02 B(chaqueM,3) B(chaqueM,3)+0.02 ;...
B(chaqueM,3) B(chaqueM,3)+0.02...
B(chaqueM,3)+0.02 B(chaqueM,3)+0.02...
B(chaqueM,3)+0.02 B(chaqueM,3)+0.02;...
B(chaqueM,3) B(chaqueM,3) B(chaqueM,3)+0.02...
B(chaqueM,3) B(chaqueM,3)+0.02 B(chaqueM,3)+0.02])
chaqueM=chaqueM+1;
end
for chaqueQ=1:q
set(graph3(chaqueQ),'XData',[C(chaqueQ,1) C(chaqueQ,1) ...
C(chaqueQ,1)+0.02 C(chaqueQ,1) C(chaqueQ,1) C(chaqueQ,1);...
C(chaqueQ,1) C(chaqueQ,1) C(chaqueQ,1)+0.02 C(chaqueQ,1)...
C(chaqueQ,1) C(chaqueQ,1) ;...
C(chaqueQ,1)+0.02 C(chaqueQ,1)+0.02...
C(chaqueQ,1)+0.02 C(chaqueQ,1)+0.02...
C(chaqueQ,1) C(chaqueQ,1)+0.02 ;...
C(chaqueQ,1)+0.02 C(chaqueQ,1)+0.02...
C(chaqueQ,1)+0.02 C(chaqueQ,1)+0.02...
C(chaqueQ,1) C(chaqueQ,1)+0.02],...
'YData',[C(chaqueQ,2) C(chaqueQ,2)+0.02...
C(chaqueQ,2) C(chaqueQ,2) C(chaqueQ,2) C(chaqueQ,2) ;...
C(chaqueQ,2)+0.02 C(chaqueQ,2)+0.02...
C(chaqueQ,2)+0.02 C(chaqueQ,2) C(chaqueQ,2)+0.02...
C(chaqueQ,2)+0.02 ;...
C(chaqueQ,2)+0.02 C(chaqueQ,2)+0.02 C(chaqueQ,2)+0.02...
C(chaqueQ,2) C(chaqueQ,2)+0.02 C(chaqueQ,2)+0.02;...
C(chaqueQ,2) C(chaqueQ,2)+0.02...
C(chaqueQ,2) C(chaqueQ,2) C(chaqueQ,2) C(chaqueQ,2)],...
'ZData',[C(chaqueQ,3) C(chaqueQ,3) C(chaqueQ,3)...
C(chaqueQ,3) C(chaqueQ,3) C(chaqueQ,3)+0.02 ;...
C(chaqueQ,3) C(chaqueQ,3)+0.02...
C(chaqueQ,3) C(chaqueQ,3)+0.02 C(chaqueQ,3) C(chaqueQ,3)+0.02 ;...
C(chaqueQ,3) C(chaqueQ,3)+0.02...
C(chaqueQ,3)+0.02 C(chaqueQ,3)+0.02...
C(chaqueQ,3)+0.02 C(chaqueQ,3)+0.02;...
C(chaqueQ,3) C(chaqueQ,3) C(chaqueQ,3)+0.02...
C(chaqueQ,3) C(chaqueQ,3)+0.02 C(chaqueQ,3)+0.02])
chaqueQ=chaqueQ+1;
end
drawnow
% code film
%mov = addframe(mov,F);
i=i+1;
%% petit graphe des concentrations
N=[N n];
M=[M m];
Q=[Q q];
I=[I i];
hold (graph2D,'on' )
graph4=plot(I,N,'-r','parent',graph2D);
graph5=plot(I,M,'-g','parent',graph2D);
graph6=plot(I,Q,'-b','parent',graph2D);
end
% code film
% mov = close(mov);
end
Les jeux vidéo (par exemple World of Warcraft) d'aujourd'hui semblent capables de contenir tant de détails, tant d'informations qu'un non expert pourrait légitimement se demander pourquoi les scientifiques n'utilisent pas ce savoir faire pour modéliser une cellule. Pourquoi ne peut-on pas, pour l'instant, créer une cellule virtuelle, une sorte de modèle tridimensionnel dans lequel on intégrerait tout (déplacement brownien des molécules, transcription, traduction, réseaux de régulation génique) ? Pour deux raisons essentiellement:
- la première c'est la puissance de calcul. Si ce modèle tridimensionnel avait une résolution spatiale de l'ordre de l'atome, la puissance de calcul nécessaire deviendrait énorme. De plus, dans le cahier des charges, voulez-vous que ce modèle soit capable de calculer le repliement des protéines à partir de la chaine d'acides aminés? je vous conseille de répondre "non" car le problème du repliement (selon le dogme actuel de minimisation de l'énergie libre) est un problème que les algorithmes actuels (ainsi que ceux du futur comme les algorithmes quantiques) ne peuvent pas traiter en un temps polynomial (un temps acceptable) à cause de l'explosion combinatoire qui augmente le nombre de calculs à réaliser de manière exponentielle avec le nombre d'acide aminés. Ainsi, en l'état actuel des connaissances, le temps de calcul du repliement d'une protéine prendrait plus de temps que l'âge de l'univers (15 milliards d'années) et ce même si l'ordinateur pouvait faire une opération, un calcul par temps de Planck (le plus petit temps possible) soit 5x10-44 s.
- La deuxième raison qui explique pourquoi on ne peut pas, pour l'instant, créer de cellules virtuelles, est liée aux problèmes fondamentaux relatifs à la complexité. On ne comprend pas encore comment un réseau biologique s'y prend pour être si robuste au bruit et si peu sensible aux conditions initiales.
Malgré ces deux raisons et parce que je suis un peu têtu, je me suis lancé dans la programmation d'une petite cellule virtuelle tridimensionnelle pour "voir" jusqu'ou je pouvais aller avant d'être bloqué.
Mon modèle ne gère pas le contact (rebond) des molécules les unes contre les autres. En revanche, la cellule virtuelle peut:
- créer des protéines ou métabolites qui se déplacent selon le mouvement brownien (l'algorithme ne décrit évidemment pas de manière parfaite ce processus: par exemple, il ne calcule pas la trajectoire correcte que prendrait une molécule après avoir rebondi contre la paroi de la cellule).
- synthétiser différents types de protéines, chacun avec un taux de synthèse respectif.
- dégrader différents types de protéines, chacun avec un taux de dégradation respectif.
- faire contrôler l'expression d'un gène via la fixation d'un facteur de transcription sur le promoteur.
La manière dont sont encodés les 3 derniers points essaie de respecter au maximum les équations déterministes décrites dans le chapitre sur la modélisation.

La raison pour laquelle je n'ai pas pu implémenter plus de fonctionnalités (et dépasser les milliers de molécules) est avant tout liée au temps de calcul. Mon algorithme n'est certainement pas optimal. Pourtant, j'ai essayé de l'améliorer de différentes manières:
- Changement de paradigme de modélisation. Une version de l'algorithme a été implémentée selon le paradigme de programmation "orienté objet" (avec des objets, des classes et des méthodes) par opposition au paradigme de programmation procédurale (avec des fonctions).
- Délocalisation des calculs sur plusieurs machines en utilisant la "parallel computing toolbox " de Matlab.
Malgré cela, mon processeur (ou mes processeurs) ne peut pas calculer en un temps raisonnable (secondes) le déplacement brownien de milliers de molécules ainsi que leur dégradation et synthèse liées aux variations d'expression génique.
L'intérêt de la programmation d'une telle cellule est de deux ordres:
- didactique: apprendre la programmation à travers un exercice relié à la biologie. Je ne pense pas cependant que le code que je fournis ait un quelconque intérêt scientifique (je suis sûr du contraire).
- paradigmatique: chaque fonctionnalité que j'encode révèle la naïveté/compréhension de ma perception d'E. coli. Ici naïveté et compréhension sont antinomiques: naïveté car de toutes façons, notre manière de voir E. coli est fausse. Il y a encore beaucoup de choses cruciales que nous n'avons pas encore comprises. Compréhension car en encodant une fonctionnalité comme la régulation d'un promoteur, vous la contrôlez (via la modification des paramètres) et donc vous commencez à la comprendre. En effet, je pense que l'on ne comprend vraiment que ce que l'on contrôle (voir le chapitre sur la biologie synthétique).
Derrière ces petits programmes "jeux en 3D" se cache une difficulté future plus profonde. Au fur et à mesure que le biologiste synthétique créera des réseaux complexes, il lui faudra avoir une estimation de plus en plus précise des paramètres. Et pour cela, il faudra créer des modèles spatiaux tridimensionnels avec une résolution de plus en plus importante. Prenons un exemple: la seule solution pour calculer précisément quelle sera l'expression d'un gène régulé par un promoteur complexe impliquant plusieurs facteurs de transcription (voir l'opéron aceBAK dans le chapitre sur la modélisation) consistera à créer un modèle pouvant simuler le contact entre les atomes de cette adénine là (base de l'ADN) avec les atomes de cette valine ci (facteur de transcription) et de faire cela pour tous les atomes impliqués. C'est, il me semble, la seule solution pour calculer/simuler/modéliser des sorties (output) complexes.
Mais on peut aussi se demander si, dans le futur, cela aura réellement un sens d'encoder autant d'informations dans un programme écrit avec un langage de programmation qui convertit l'information en bit (software) pour un ordinateur composé de transistors (hardware). En effet, il se pourrait bien que, dans le futur, l'ordinateur chargé d'évaluer la sortie (l'output) du promoteur complexe ne soit plus un ordinateur classique mais la cellule elle-même: le Wetware.
Enfin, et je terminerai mon chapitre avec cette question: peut-on concevoir une cellule virtuelle parfaite in silico avec un programme fait de 0 et de 1 ? Et si cette cellule existait, qu'est que ce qui la distinguerait d'une cellule réelle ? Si on peut créer une cellule avec de 0 et des 1, on peut créer des organismes multicellulaires avec des 0 et 1, puis des hommes avec des 0 et 1. Qu'est que ce qui distinguerait ces hommes in silico des hommes réels ?
Bibliographie
- Becskei, A. and L. Serrano (2000). "Engineering stability in gene networks by autoregulation." Nature 405(6786): 590-3.
- Bigger, J. (1944). "Treatment of staphylococcal infections with penicillin by intermittent sterilisation." Lancet.
- de Jong, H. and F. Rechenmann (2005). "Et la cellule devint virtuelle " La recherche.
- Elowitz, M. B., A. J. Levine, et al. (2002). "Stochastic gene expression in a single cell." Science 297(5584): 1183-6.
- Gillespie (1977). "Exact stochastics simulation of coupled chemical reactions."
- Isaacs, F. J., J. Hasty, et al. (2003). "Prediction and measurement of an autoregulatory genetic module." Proc Natl Acad Sci U S A 100(13): 7714-9.
- Kupiec, J.-J. (2009). "L'ADN entre hasard et contraintes." pour la science.
- Lindner, A. B., R. Madden, et al. (2008). "Asymmetric segregation of protein aggregates is associated with cellular aging and rejuvenation." Proc Natl Acad Sci U S A 105(8): 3076-81.
- Mihalcescu, I., W. Hsing, et al. (2004). "Resilient circadian oscillator revealed in individual cyanobacteria." Nature 430(6995): 81-5.
- Novick, A. and M. Weiner (1957). "Enzyme Induction as an All-or-None Phenomenon." Proc Natl Acad Sci U S A 43(7): 553-66.
- Stewart, E. J., R. Madden, et al. (2005). "Aging and death in an organism that reproduces by morphologically symmetric division." PLoS Biol 3(2): e45.
- Thattai, M. and A. van Oudenaarden (2001). "Intrinsic noise in gene regulatory networks." Proc Natl Acad Sci U S A 98(15): 8614-9.
Notes de bas de page
- La plupart des protéines d'une cellule sont présentes en moins de dix exemplaires.
- Ce que nous appelons aujourd'hui boucle de rétroaction positive.
- Je mets déterministe entre guillemet car en réalité, les équations maitresses, malgré la présence de probabilités, sont également déterministes.
- La traduction du verbe "to plot" en français est "tracer" mais je préfère franciser le mot anglais en "plotter". De même, la traduction du verbe "to fit" en français est "ajuster" mais je préfère franciser le verbe en "fitter".
- Je fais exprès d'utiliser le verbe "implémenter" (champ lexical de l'informatique) en parlant d'une construction synthétique réelle pour inciter les biologistes synthétiques expérimentalistes à apprendre à penser, quand cela est nécessaire, en informaticien. Ils doivent apprendre à jongler entre les champs lexicaux de la biologie et de l'informatique/mathématique.
- La photo de microscopie électronique est issue de Wikipedia: article sur E. coli.