L'information en biologie

La notion d'information

Nous avons vu, dans le chapitre précédent, que le cerveau, par l'intermédiaire de l'oeil humain, accorde une plus grande quantité d'information à certaines images qu'à d'autres. Mais qu'appelle-t-on exactement information ? En général, quand on parle d'information, on parle d'une chaine de caractère. Il peut s'agir de nos journaux quotidiens, du code secret de ma carte bancaire, des suites de caractères présents dans l'ouvrage La barque de Delphe¹, de la suite des notes d'une mélodie agréable, des suites de caractères du dernier programme que je vous ai décrit, de coordonnées GPS des emplacements de tous les "Mac Donald" sur le territoire français. Bref, ce mot information est très large: il englobe beaucoup de choses. Pourtant, il me semble que le concept d'information effraie parfois les biologistes car il est souvent associé aux mathématiques via les fameuses "théories de l'information". Dans ce chapitre, j'aurai atteint mon but si je réussis à convaincre des biologistes que pour comprendre l'essence même de ces théories, il n'est pas forcement nécessaire de comprendre les équations associées ---Soyez bien certain d'ailleurs que je ne les comprends pas---.

En revanche, il y a deux choses dont il faut avoir conscience:

• La limitation intrinsèque des théories actuelles de l'information: il n'existe pas de théorie de l'information de valeur² capable de s'intéresser à la signification d'un message.
• Quand on parle d'information, on peut très vite faire de la métaphysique déguisée derrière des mathématiques ---et ce n'est pas un problème à condition d'en avoir conscience---.

Dans l'exposé qui suit, je vais poser une question:

"Quelle peut être l'information associée à un génome ?"

Je vais tout d'abord tenter de décrire quelle sont les apports des théories actuelles pour évaluer l'information contenue dans un génome. Puis je développerai un point de vue personnel pour essayer d'aller plus loin. Chacun sera libre de fixer librement le curseur entre science et métaphysique.

La théorie de l'information de Claude Shannon

Par où commencer ? Je vous propose de commencer par télécharger, via Matlab, la séquence du génome d'E. coli (Figure 1). J'enregistre ensuite cette séquence sur mon disque dur: celle-ci fait 9.2 Méga-octets pour un fichier texte de 4 639 675 paires de bases. Maintenant, je crée une séquence aléatoire de même taille (4 639 675 pb), je l'enregistre sur mon disque dur et, surprise, celle-ci fait exactement la même taille: 9.2 Mo.

A partir de là, deux questions apparaissent:

• Pourquoi ces séquences font-elles 9.2 Mo sur mon ordinateur ?
• Pourquoi la séquence du génome d'E. coli et une séquence aléatoire font-elles la même taille ?

Pourquoi 9.2Mo ?

La place qu'occupe tout fichier sur un ordinateur peut être calculée en utilisant la théorie de l'information dont Claude Shannon est le père fondateur avec son article A Mathematical Theory of Communication publié en 1948. L'équation principale de la théorie de l'information est:

I=k.log2(P)

Dans notre cas, I représente la quantité d'information (en bit) présente, selon Shannon, dans la séquence d'ADN de taille k et où P est la probabilité d'apparition d'un nucléotide donné.

Par exemple, pour une séquence d'un seul nucléotide "A", on a:

I=1xlog2 (0.25) = 2 bit car il y a 4 nucléotides possibles (A, T, C, G) dont une chance sur 4 (0.25) d'avoir un A.

Pour le génome d'E. coli (4 639 675 nucléotides) on a:

I= 4 639 675 x log₂(0.25)=4 639 675 x 2 = 9 279 350 bit

Or un octet fait 8 bits, on a donc:

I= 9 279 350 /8 = 1.16 Mega octet.

C'est la taille minimum que peut prendre le génome d'E. coli sur un disque dur sans compression. Cependant, les éditeurs de texte encodent chaque caractère sur 8 bits (256 possibilités de lettres/symboles différents) pour pouvoir gérer le grand nombre de lettres de l'alphabet. La séquence d'E. coli fait donc finalement:

I= 1.16 x 8 = 9.28 Mega-octet.

Pourquoi la séquence du génome d'E. coli et une séquence aléatoire font-elles la même taille ?

La théorie de l'information, de l'aveu même de son fondateur, n'est pas vraiment une théorie de l'information mais plutôt une théorie de la communication. Cette théorie est très utilisée pour coder et transmettre un message en bits mais elle exclut totalement la sémantique: elle est donc totalement indifférente à la signification des messages. Le sens d'un message peut pourtant être considéré comme essentiel dans la caractérisation de l'information. Par exemple, les informations présentes dans les phrases "sort ! Il y a le feu !", "Sort ! Il y a le car !" et "sgrt e ij n a he dje r" ne possèdent pas, à l'évidence, les mêmes valeurs. Or cette "valeur", la théorie de l'information de Shannon ne pourra pas la mesurer: tous ces messages font 176 bits. De la même manière, nous ressentons intuitivement que le génome d'E. coli contient bien plus d'information qu'une séquence aléatoire de même taille car ce vrai génome contient l'information capable de générer une entité auto-réplicative alors que la séquence aléatoire n'est qu'une suite de symboles choisis au hasard.

La théorie algorithmique de l'information de Kolmogorov

Encore une fois, cette théorie ne va pas pouvoir mesurer la "valeur" d'une information mais elle va pouvoir mesurer sa compressibilité. En effet, l'idée principale de la théorie algorithmique de l'information est qu'une chose est d'autant plus complexe, ou contient d'autant plus d'information, qu'elle est difficile à expliquer, c'est-à-dire fondamentalement longue à expliquer.

Par exemple, la séquence ADN:

AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAA

a une description courte "30 répétitions de A" alors que la séquence aléatoire:

ATCGTGGGCTAGGGGTACGCGCCATCGATC

n'a apparemment pas de description plus simple que la chaine de caractère elle-même.

Ainsi, du point de vue de la théorie algorithmique de l'information, découverte dans les années 60, l'information présente dans une chaine de caractère est équivalente à la longueur de la plus courte représentation de cette chaine de caractère. Or cette représentation courte est essentiellement un programme qui, lorsqu'il s'exécute, fournit la chaine de caractère en "ouptut".

Ainsi, la complexité algorithmique (dite complexité de Kolmogorov) d'une chaine de caractère x est définie comme la longueur du plus petit programme qui "compute" x.

Par conséquent, une chaine de caractère dont la complexité de Kolmogorov est petite, relativement à la taille de la chaine de caractère correspondante, n'est pas considérée comme complexe/informative.

La complexité de Kolmogorov permet de définir formellement le concept "aléatoire". En effet, une chaine de caractère est dite "aléatoire" si et seulement si elle est plus petite que n'importe quel programme capable de la générer.

Ainsi, selon cette théorie, ce qui est complexe, ce qui contient de l'information, c'est ce qui est aléatoire: on parle de complexité aléatoire. Vous voyez que cette manière de pensée rentre en contradiction avec nos intuitions en biologie: pour nous, un organisme vivant est très complexe sans pour autant que l'on se représente cette organisme comme étant essentiellement composé de hasard.

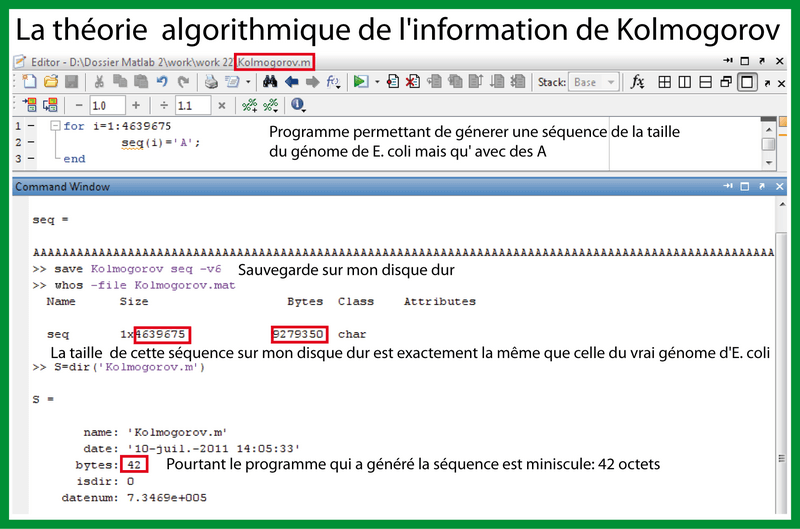
Pour être sûr que vous ayez bien compris la théorie algorithmique de l'information, je vous ai concocté un petit exercice "pratique" relatif au génome. Sur la figure 2, vous pouvez voir un petit script que j'ai appelé Kolmogorov.m (le programme) qui consiste en une boucle qui écrit 4 639 675 fois le nucléotide A. Si je sauve cette séquence de A sur mon disque dur (Kolmogorov.mat ; la séquence) je tombe sur l'information de Shannon (9.2Mo). Cependant, le programme Kolmogorov qui m'a permis de générer cette séquence ne fait, lui, que 42 octets. Il représente une description de la séquence beaucoup plus courte que la séquence elle-même. Ainsi selon Shannon, la séquence du génome de E. coli et une séquence de "A" de même taille contiennent la même information (9.2Mo) alors que, selon Kolmogorov, la séquence de "A" est beaucoup plus simple/moins informative ce que nous, biologistes, ressentons effectivement intuitivement.

La profondeur logique de Bennett

La profondeur logique de Bennett est un concept de logique informatique mentionnée dans un article de Gregory Chaitin en 1977 qui l'attribue au physicien et logicien américain Charles H. Bennett.

Ce concept diffère de la complexité de Kolmogorov dans le fait qu'il considère le temps de calcul de l'algorithme le plus court, plutôt que sa longueur.

Soit une chaine de caractères x, P(x) est le temps de calcul du programme minimal de x.

Le temps de calcul est lié à la présence de boucles (par exemple, la boucle for) et donc à la présence d'itérations. Ainsi l'information contenue dans un algorithme s'y trouve à l'état potentiel. Elle nécessite un temps plus ou moins long pour en être extraite.

Comme la complexité de Kolmogorov, la profondeur de Bennett est approchable mais n'est pas calculable (la fonction x -> P(x) n'est pas récursive). La profondeur logique est donc sujette à de fortes propriétés d'indécidabilité.

Cependant, la profondeur logique apporte une nouvelle dimension à la mesure de la complexité. La notion de complexité organisée (profondeur logique) par opposition à la complexité aléatoire (complexité de Kolmogorov). En effet, la profondeur logique mesure la présence de structures, d'organisation et donc elle diminue avec l'aléatoire alors que la complexité de Kolmogorov, elle, augmente avec l'aléatoire (absence de structure). Autrement dit, l'incompressibilité entraîne la rapidité du calcul.

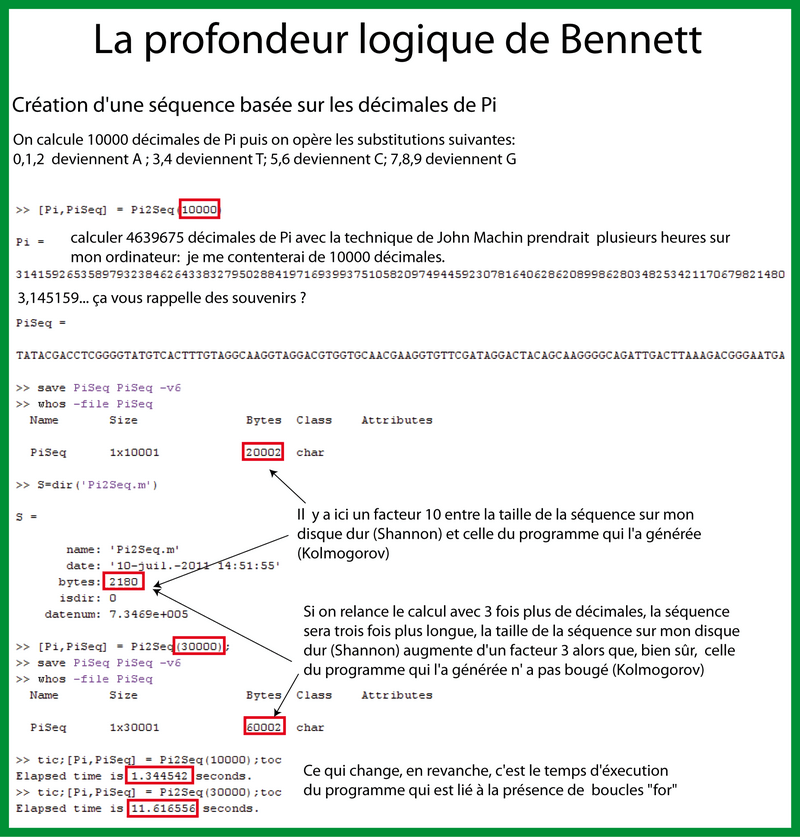
Je vais illustrer ces idées à l'aide de mon exemple relatif au génome illustré sur la figure 3. Je dispose d'un script Matlab, trouvé sur Internet, qui calcule les décimales de Pi en utilisant la méthode de John Machin. Je donne au script le nombre de décimales de Pi que je veux connaître, puis une fois le programme exécuté, celui-ci me "renvoie" la suite de ces décimales calculés:

31415926535897932384626433832795028841971693

Puis, grâce à quelques lignes de code ajoutées dans le script, ce dernier substitue les entiers par les bases ADN selon le plan suivant:

0,1,2 deviennent A ; 3,4 deviennent T ; 5,6 deviennent C et 7,8,9 deviennent G.

On obtient alors la séquence suivante qui, en quelque sorte, est un reflet de Pi:

TATACGACCTCGGGGTATGTCACTTTGTAGGCAAGGTAGGACGT

Pour 10 000 décimales (je ne le fais pas cette fois pour 4 639 675 décimales car cela prendrait plusieurs heures), la séquence, enregistrée sur mon ordinateur fait 20ko alors que le programme qui calcule Pi ne fait que 2 ko. Ainsi selon la théorie algorithmique de l'information de Kolmogorov, cette séquence est moins compliquée qu'une séquence aléatoire incompressible. Si maintenant, je relance le calcul en demandant non pas 10 000 mais 30 000 décimales, la taille de la séquence générée sera bien 3 fois plus grande sur mon disque dur (selon la théorie de l'information de Shannon) c'est-à-dire 60 ko. Bien sûr, la taille du programme calculant Pi n'a pas changé et fait toujours 2 ko. Or intuitivement, on ressent bien que connaître 30 000 décimales de Pi est plus informatif que de n'en connaître que 10 000. Et cette intuition là, la complexité de Kolmogorov ne peut pas la capter. Pour prendre en compte, cette complexité dite organisée, on utilise le concept de profondeur logique. En effet, le temps d'exécution du programme pour calculer les 10 000 décimales est de l'ordre de 1 seconde alors qu'il faut 10 secondes pour en calculer 30 000. Ainsi, les boucles "for" présentes dans le programme font que la séquence basée sur Pi a une forte complexité organisée (long temps de calcul) mais une faible complexité aléatoire (la taille du programme est petite).

Synthèse en image: Shannon, Kolmogorov, Bennett

Pour être sûr que les différences entre ces trois manières d'envisager la complexité (l'information) sont claires dans l'esprit de mon lecteur, je vais donner un dernier exemple basé sur des images.

Sur la figure 4, on observe 3 images: une image uniforme (toute noire), une image aléatoire (composée de pixels blancs et noirs placés aléatoirement) et une image correspondant à l'ensemble de Mandelbrot (une fractale populaire) en noir et blanc également. Selon la théorie de l'information de Shannon, ces trois images contiennent autant d'information. En effet, elles font toutes exactement 230 ko car le nombre de pixel (520x420) est identique dans les trois cas. Selon Kolmogorov, l'image uniforme est la plus simple car le programme qui la génère ne fait que 51 Ko. L'image de l'ensemble de Mandelbrot nécessite, quant à elle, un programme de 182 ko. L'image aléatoire est générée par un programme court mais ce dernier intègre la fonction rand (fonction qui crée du hasard) or cette fonction injecte de l'information dans le système. Le script ne contient donc pas, en lui-même, la description de l'image car si on l'exécute deux fois suites, il y aura deux images différentes. La seule manière de faire réapparaitre l'image, c'est d'indiquer au programme la valeur des 520x420= 218400 pixels ce qui au final, ne représente pas une compression et nous ramène à l'information selon Shannon soit 230ko (plus une constante). Ainsi, selon, la théorie algorithmique de l'information de Kolmogorov, l'image la plus complexe/informative est l'image aléatoire (elle est incompressible ; c'est la complexité aléatoire), vient ensuite l'ensemble de Mandebrot puis enfin, l'image uniforme qui est celle qui contient le moins d'information.

Etudions maintenant le temps nécessaire pour générer ces images: les images uniformes et aléatoires sont générées en moins d'une seconde alors que l'ensemble de Mandelbrot a nécessité plus de 20 secondes. Cette dernière image a une plus grande profondeur logique selon Bennett. On parle de complexité organisée. En effet, cette image, par rapport aux deux autres, possède une structure, une organisation. Ce sont donc ces structures liées à la profondeur logique d'un programme qui nous rappellent le plus les êtres vivants. Ce sont elles qui sont, à notre sens, les plus informatives.

                
F=figure('Color', 'w');
for i=1:3  % genere 3 petit plots 
    Handle(i)=subplot(1,3,i);
    hold(Handle(i));
end
% Image 1 uniforme noir
axes(Handle(1));
cdata=uint8(zeros(420,560));
imshow(cdata);
figure;
cdata=uint8(zeros(420,560));
imshow(cdata);
saveas(gcf,'imageUniforme','bmp');
clear cdata;
% Image 2 aleatoire
axes(Handle(2));
cdata=uint8(rand(420,560)*256);
imshow(cdata);
figure;
imshow(cdata);
saveas(gcf,'imageAleatoire','bmp');
clear cdata;

% Image 3 : ensemble de Mandelbrot
x = linspace(-2.1,0.6,1000);
y = linspace(-1.1,1.1,1000);
[X Y] = meshgrid(x,y);
C = complex(X,Y);
Zmax= 2;
kmax= 50;
Z = C;
for k=1:kmax
Z = Z.^2 + C;
end
contourf(x,y,Z);
axis off;
colormap gray;
saveas(gcf,'imageMandelbrot','bmp');
imread('imageMandelbrot.bmp');
axes(Handle(3));
imshow(ans);
imshow(F);
saveas(gcf,'Information3Images2','eps');


                
            

Voyons maintenant pourquoi. Commençons tout d'abord par résumer ces 3 manières de conceptualiser l'information:

• La théorie de Shannon postule que le génome d'E. coli contient autant d'information qu'un génome aléatoire
• La théorie de Kolmogorov propose de tenter de "compresser" le génome d'E. coli avec un programme pour évaluer sa complexité algorithmique
• La théorie de Bennett propose d'évaluer le temps nécessaire pour générer ce génome (Bennett).

Les biologistes dressent immédiatement un pont entre le troisième point et la théorie de l'évolution. En effet, le temps nécessaire pour générer le génome actuel d'E. coli correspond aux milliards d'années du temps évolutif, c'est-à-dire des milliards de cycles de réplications / mutations / sélection. Je tiens cette idée d'Antoine Danchin ³ :

                

% petit script didactique pour montrer que la profondeur logique de
% chaque nucleotide augmente au cours de l'evolution
scrsz = get(0,'ScreenSize');
F=figure('Color','w','Position',[0 0 scrsz(3) scrsz(4) ]);
%mov = avifile('ProfondeurLogique3.avi','quality',100,'compression',...
%    'none','fps',5);% code film
g1=subplot(1,2,1);
xlabel('Temps (millions d années)','FontSize',18);
ylabel('Profondeur logique/Complexité organisée/Information','FontSize',18)
hold(g1);
set(g1,'XTick', []);
set(g1,'YTick', []);
axis square;
axis on;
g2=subplot(1,2,2);
axis([1 3 1 3]);
axis square;
axis off;

Sequence(1:90)='A';
% cree un matrice de place aleatoire dans le plasmide (entre 1 à 90pb). sa
% taille depend de nombre de bacteries qui mutent
Place= randi(90,[1,1500]);
% cree matrice de base string de la même taille que place (même proba pour
% chaque base d'apparaitre)
Base=randsample('ACGT', 1500,true,[0.5 0.5 0.5 0.5]);

Cercle=0:pi/45:2*pi;
Fitness=1;
hold on
for Indice=1:90
    h{Indice}=text(2+cos(Cercle(Indice)),2+sin(Cercle(Indice)),...
        Sequence(Indice),'FontSize',16);% sinon base noir
end
for i =1:300
    if rand(1)>0.75
        delete(h{Place(i)});
        h{Place(i)}=text(2+cos(Cercle(Place(i))),2+...
            sin(Cercle(Place(i))),Base(i),'FontSize',16,'Color','g');       
        if i>1
            Fitness(i)=Fitness(i-1)+1;
        end      
    else
        Green=get(h{Place(i)},'Color');
        
        if ~strcmp(num2str(Green),'0  1  0')
            delete(h{Place(i)});
            h{Place(i)}=text(2+cos(Cercle(Place(i))),2+...
                sin(Cercle(Place(i))),Base(i),'FontSize',20,'Color','r');
            
            pause(0.08);
%             frame = getframe(F);             
%             mov = addframe(mov,frame);% code film
            delete(h{Place(i)});
            h{Place(i)}=text(2+cos(Cercle(Place(i))),2+...
                sin(Cercle(Place(i))),Sequence(Place(i)),...
                'FontSize',16,'Color','k');
        end  
        if i>1
            Fitness(i)=Fitness(i-1);
        end   
    end
    plot(g1,1:i,Fitness(1:i))  ;
end
%mov = close(mov);% code film
                
            

A partir de là, il me semble que tout scientifique qui souhaite approfondir le concept d'information (en lien avec la biologie) doit se frayer un chemin, par lui-même, dans la jungle de l'inconnu. Il dispose pour l'aider de quelques outils (ses machettes) que sont les fondements des 3 théories décrites. Cependant, pour explorer l'inexploré, il devra nécessairement en inventer de nouveaux. Il me semble que ce constat est également partagé par Antoine Danchin ou plus exactement, je le partage avec Antoine Danchin. En effet, c'est après avoir lu son "appel" ci-dessous (diffusé depuis son site web) que j'ai souhaité réfléchir à ce problème de l'information de valeur. Autrement dit, j'ai souhaité répondre à son appel à ma manière.

Spéculation personnelle sur l'information

Pour débuter mon exploration dans la jungle, j'ai commencé par une intuition: tout biologiste pense que le génome d'E. coli (9.2Mo selon Shannon) contient beaucoup plus d'information de valeur qu'une séquence aléatoire de même taille (9.2Mo). La piste " Kolmogorov" nous oriente vers la compression de ce génome alors qu'il faut penser rigoureusement dans la direction opposée: il faut décompresser ce génome. Autrement dit, à ce génome de 9,2 Mo n'est pas associé un programme plus petit (en bit) (la complexité de Kolmogorov) mais une Information Décompressée bien plus grande (toujours en bit) que j'appellerai ID dans la suite de mon exposé. Je partirai donc du postulat suivant:

ID existe, c'est une chaine de caractère de taille finie, en bit.

Ce postulat est basée sur:

• l'intuition d'existence:

  ID (séquence du génome d'E. coli)> ID (séquence aléatoire de même taille)

• l'intuition qu'ID a une taille finie

  ID (séquence du génome humain)>ID (séquence génome d'E. coli)

La taille de l'information décompressée du génome humain semble intuitivement bien supérieure à celle du génome d'E. coli. En cela, elle constitue une borne, une limite supérieure vers le haut prouvant qu'ID (E. coli) est une séquence de taille finie et non infinie. Je me dois cependant de reconnaitre ici ma crainte de la faiblesse du raisonnement mathématique.

L'existence de ID peut être aussi entrevue par une expérience de pensée: la découpe d'un génome en morceaux de plus en plus petit. En effet, en coupant au fur et à mesure de deux en deux le génome d'E. coli, on crée des séquences de 4 600 000 bases, 2 300 000 puis 1 150 000 ... 64, 32, 16, 8, 4 ,2 ,1 nucléotides (illustré sur la figure 6). Selon Shannon, cette découpe divise symétriquement par deux, de manière constante, le contenu en information des séquences correspondantes. Or dès la première découpe, on passe d'une séquence pouvant générer la vie (un système auto-réplicatif) à une séquence incapable de générer la vie. La perte d'information est bien supérieure à un facteur 2. Puis cette perte d'information au fur et à mesure des découpes diminue: elle n'est donc pas constante. Elle tend vers la perte de Shannon (facteur deux) qu'elle atteint lors de la dernière découpe (de 2 bases à 1 base).

D'où vient ID ? Et pourquoi la perte d'information décroit-elle, intuitivement, au fur et à mesure des découpes ? Pourquoi y a-t-il plus d'informations dans le génome d'E. coli que dans un génome aléatoire de même taille ? Parce que les cycles de réplications/mutations/sélection au cours de plusieurs milliards d'années d'évolution ont engendré des nucléotides avec une grande profondeur logique. Cette profondeur logique se caractérise par des interactions/liens virtuels entre nucléotides.

Je m'explique: commençons avec un cas simple (figure 7):

Nous avons vu que le principe d'un réseau de régulation génique est simple: un gène A codant pour un facteur de transcription peut contrôler la transcription d'un autre gène B. Autrement dit, les nucléotides du gène A ont un lien invisible, virtuel avec les nucléotides du gène B. Ce lien ne peut apparaitre que lors de l'évaluation/l'exécution du programme (la vie de la bactérie E. coli, la dynamique). Il n'empêche que ce lien virtuel existe, a priori, sur la séquence statique avant toute exécution. Et c'est ce type de lien, inexistant dans une séquence aléatoire, qui génère un surplus d'information " à ajouter" à l'information minimale de Shannon.

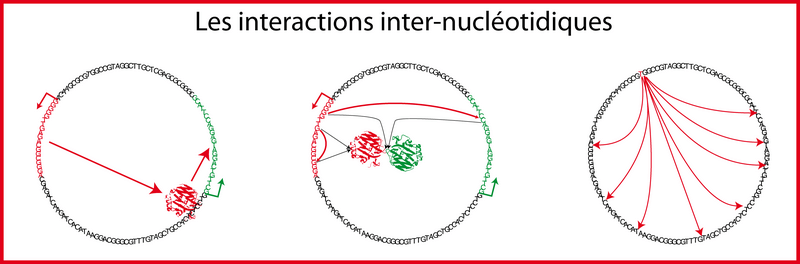
Ces interactions ne se limitent pas aux interactions des réseaux de régulation génique: ce sont des interactions dans un sens plus large. Le nucléotide numéro 235 d'un gène a une interaction virtuelle avec le nucléotide numéro 747 si les deux acides aminés se retrouvent côte à côte lors du repliement et forment une liaison chimique. Même raisonnement si deux nucléotides appartenant à deux gènes différents se retrouvent, une fois sous forme d'acide aminé, en contact physique (par exemple lors de transduction du signal). Ce sont vraiment des interactions virtuelles au sens large: les nucléotides d'un gène codant pour une enzyme impliquée dans la biosynthèse des lipides ont une interaction virtuelle avec tous les nucléotides des gènes codant des protéines. En effet, la membrane (composée de lipides) limite physiquement la diffusion dans l'espace de ces protéines. Notez aussi que ces interactions virtuelles ont toujours une réalité physique lors de l'exécution du programme. Cette réalité physique c'est toujours, quoi qu'il arrive une liaison physique: le facteur de transcription touche vraiment le promoteur (et matérialise par là la liaison virtuelle entre les nucléotides correspondants), les acides aminés sont vraiment en contact dans la protéine repliée, les lipides empêchent vraiment les protéines de sortir.

Vous comprenez donc bien que le nombre d'interactions de ce type est astronomique (mais, il me semble, fini). En fait, chaque nucléotide a potentiellement un impact / une interaction virtuelle / un lien avec l'ensemble des autres nucléotides. C'est ce réseau dense de liens invisibles qui engendre l'information cachée dans la séquence. Dans une séquence aléatoire en bit, chaque bit est strictement indépendant des autres bits par définition. Ce n'est pas le cas dans une séquence génomique: les bits sont reliés par des fils invisibles. Le fil devient visible lorsque la liaison physique se matérialise et cela ne se produit que lors de l'exécution dynamique du programme.

Nous avons donc vu qu'à une séquence ADN en bits (en fait, une base ADN contient 2 bits ; on peut donc parler de séquence ADN en bases ou en bits) est associée une chaine de caractères également en bits, bien plus grande, et nommée I Décompressé. A partir de là, qu'est ce qui m'empêche de postuler qu'il existe une fonction f tel que:

ID_E.coli=f(séquences du génome de E. coli)

Ainsi que la fonction réciproque (pas au sens mathématique ; ou du moins, je n'en sais rien)

Séquence du génome de E. coli = f^-1(ID)

Pour l'instant, pour avoir accès à ID, on décompresse l'information de la séquence à l'aide de la cellule elle-même. C'est ce que les biologistes font expérimentalement tous les jours. La cellule (la machine) interprète le programme (la séquence) ce qui crée des phénotypes. Ce sont ces phénotypes mis bout à bout qui représentent ID en quelque sorte: ID c'est la description la plus courte de l'ensemble des interactions virtuelles entre nucléotides de telle sorte que les bits de cette description soient strictement indépendants (ce qui n'est pas le cas dans la séquence ADN). Les publications scientifiques, les bases de données qui décrivent des interactions, des phénotypes sont une part (infime) d'ID. Evidemment, cette part infime ne représente pas la description "la plus courte" et pourrait donc être compressée. Avant de commencer ma thèse, j'ai été attiré par l'idée, un peu naïve, de créer une cellule "virtuelle" dans l'ordinateur c'est-à-dire de réaliser un modèle tridimensionnel d'une cellule qui soit le plus proche possible de la réalité. Ce type de modèle pourrait, dans l'idéal, décrire le fonctionnement du réseau et reproduire l'ensemble des phénotypes de la bactérie. Ce qui est important de constater, c'est que ce programme (l'algorithme) de cellule virtuelle aussi parfait qu'il puisse devenir, risque d'être, de l'ordre de grandeur d'ID c'est-à-dire potentiellement astronomique. Tous les modèles dynamiques actuels contiennent la description d'une part infime d'ID, pas la description de la séquence ADN !

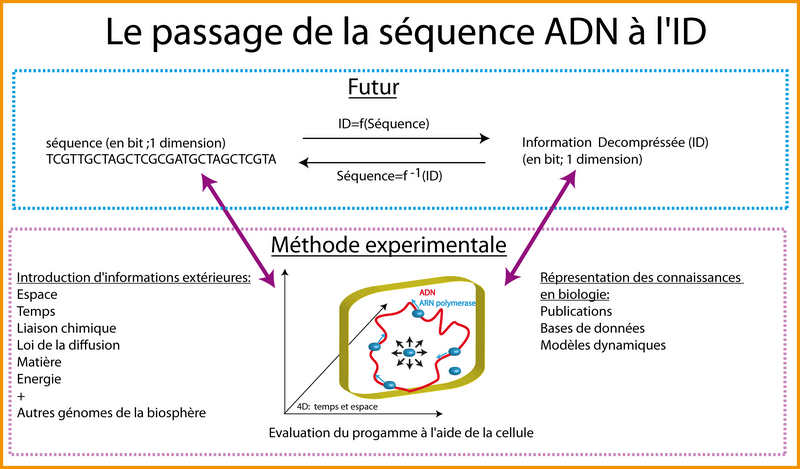
Je souhaite maintenant préciser un point important. Lorsque la cellule est utilisée pour exécuter le programme (la séquence), il y a introduction/injection d'informations étrangères au génome. Antoine Danchin appelle cette information l'information du châssis (Danchin, 2009). Je souhaite découper cette information en trois types (découpage arbitraire car les éléments peuvent être placés dans plusieurs catégories):

• Information d'origine physique: il s'agit du temps, de l'espace, les lois relative à la matière et l'énergie (liaisons chimiques), les lois de la diffusion et j'en oublie.
• Information d'origine biologique: ou plutôt relative au milieu: PH, température, conditions initiales du contenu cellulaire. Ces dernières sont importantes pour les questions relatives au bruit (multi-stabilité).
• Information d'origine métaphysique: via l'introduction de hasard (de libre arbitre !) lié aux échelles de l'infiniment petit (déplacement aléatoire des molécules selon le mouvement brownien)

La méthode qu'utilise la cellule pour compresser ID en séquence ADN devrait intéresser de plus prés la communauté scientifique et en particulier les mathématiciens car la "nature" semble disposer d'une capacité de compression de l'information prodigieuse. Rendez-vous compte en imaginant la taille gigantesque de l'ID des humains: cette ID est compressée en une séquence de 3 milliards de bases, ce qui tient sur un DVD. Or une simple "pensée humaine" pourrait être assimilée à un phénotype et donc faire partie de cette ID même si l'introduction de hasard dans le processus (et donc potentiellement d'information) me fait douter sur ce point mais cela à l'avantage de nous laisser un petit peu de libre arbitre 😀.

Les mathématiciens ne devraient-t-il pas regarder de plus prés comment la nature s'y prend pour incorporer plus d'information que celle de Shannon dans une chaine de caractère ? Ne devraient-ils pas s'intéresser de plus prés à ce que représentent ces interactions virtuelles entre nucléotides/bits ? Quel est le socle théorique nécessaire pour pouvoir procéder à ce type de compression ? Par exemple, la machine capable de compresser et décompresser doit-elle forcement avoir des caractéristiques similaires à celles de la cellule ? C'est-à-dire:

• calcul parallèle et probabiliste ?
• support/réalité physique (les interactions virtuelles doivent se concrétiser dans la réalité physique cellulaire: c'est la liaison/le contact physique entre entités) ?

Cette question du support physique me semble importante: peut-on réellement imaginer qu'une machine de Turing (ordinateur) puisse prendre en argument la séquence et ressortir l'ID en output et réciproquement, ce qui revient, d'une certaine manière, à by-passer, la réalité physique ?

J'ai proposé ci-dessus une petite application qui permettrait de compresser ou décompresser une quantité d'information astronomique en essayant de reproduire la méthode qu'utilise la nature. Mais cette petite application est l'arbre qui cache la forêt. Les conséquences sur l'homme et plus généralement sur la vie si cette fonction (et sa réciproque) existait et si on la découvrait (ou si on l'approchait) serait gigantesques: ces conséquences dépassent l'entendement. Par exemple, l'utilisation de cette fonction nous permettrait d'accroitre nos capacités cognitives de manière prodigieuse ce qui permettrait de "construire" de nouveaux objets mathématiques pour l'instant non constructibles par nos cerveaux actuels. Mais je réserve cette partie beaucoup trop métaphysique pour le chapitre sur le futur lointain.

Il me faut maintenant rentrer un peu plus en profondeur, là où se logent les difficultés. Là où le lecteur risque de subir le brouillard qui se loge dans ma tête. Il ne devrait se lancer dans la lecture des paragraphes qui suivent que si la lecture des paragraphes précédents lui a semblé relativement facile. Vous voilà " informé" 😀.

J'identifie deux questions difficiles (où je ne peux fournir que des éléments de réponses incomplets voire faux)

• Quels sont les objets mathématiques qui décrivent les interactions/liens virtuels entre nucléotides ?
• La fonction qui transforme une séquence ADN en ID et sa réciproque sont-elles vraiment calculables (récursives) ?

Quels sont les objets mathématiques qui décrivent les interactions/liens virtuels entre nucléotides ?

Pour répondre à cette question, il me faudrait sans doute l'aide d'un mathématicien. Je donne un certains nombres de pistes sans connaitre la bonne réponse et sans même savoir s'il y en a une (figure 9).

Un nucléotide a potentiellement un lien avec l'ensemble des nucléotides du génome. On peut donc imaginer, pour chaque nucléotide, l'existence d'un vecteur de taille [taille(génome)-1] dont chaque élément de ce vecteur décrit l'interaction de ce nucléotide avec un autre nucléotide (cette interaction peut très bien être nulle, inexistante). Cet élément, cette interaction particulière, c'est une fonction qui prend en argument l'ensemble de la séquence. Car la manière dont un nucléotide interagit avec un autre nucléotide dépend des autres [taille (génome)-2] nucléotides. Vous voyez que les capacités d'abstraction sont mises à rude épreuve. Premièrement, je suis gêné par l'incertitude concernant la présence ou l'absence de récursivité dans le phénomène que je décris. Deuxièmement, j'ai des difficultés à voir si un nucléotide a potentiellement un lien avec l'ensemble des nucléotides du génome ou si un nucléotide a potentiellement un lien avec l'ensemble des ensembles des nucléotides du génome. Enfin, le génome, à l'évidence, encode des phénomènes de multi-stabilité (voir le chapitre sur le bruit) et je ne sais pas si ceux-ci représentent une difficulté supplémentaire.

La fonction qui transforme une séquence ADN en ID et sa réciproque sont-elles vraiment calculables (récursives) ?

La manière de formaliser les liens virtuels entre nucléotides permet de postuler l'existence d'un supremum à l'information décompressée d'un génome que nous appellerons IDM (Information Décompressée Maximum). Cette IDM correspond au nombre maximum atteignable d'interactions entre nucléotides.

Toute séquence A de n bits (compressée ; bits non indépendants les uns des autres) associe une séquence B (nommée IDM) de m bits (décompressée ; bits indépendants ; m>>n) tel qu'il est impossible de rajouter de l'information (des bits) dans B sans devoir en rajouter dans sa version compressée A.

Notez que l'ID d'un génome donné est, le plus souvent, bien inférieur à l'IDM: toutes les interactions possibles entre bits ne sont pas forcement utilisées dans un génome donné: la "matrice peut très bien être creuse". De plus, pour deux génomes de même taille (approximativement), par exemple le chimpanzé et l'homme, nous ressentons bien (d'ailleurs un peu prétentieusement) que l'ID de l'homme est supérieure à l'ID du chimpanzé, à cause des facultés des deux cerveaux qui sont très différentes. Cela montre bien que pour une séquence x d'une taille donnée, il existe un IDM tel que tout génome (passé, présent et futur) de taille x a une ID inférieure ou égale à l'IDM. Notez que si l'IDM n'existait pas, quel intérêt aurait la nature à augmenter la taille des génomes pour augmenter la complexité des organismes ? (taille du génome de E. coli: 4 millions de bases ; taille du génome humain: 4 milliards de bases soit une différence de taille d'un facteur 1000). Il suffirait à la nature de garder la taille des génomes constante et de se contenter d'accroitre la profondeur logique des nucléotides, d'accroitre indéfiniment le nombre d'interactions virtuelles entre nucléotides. On vivrait dans un monde où le génome d'E. coli et celui de l'homme feraient la même taille mais où celui de l'homme serait beaucoup plus profond, contiendrait bien plus d'informations cachées.

Mais pourquoi m'acharner à vous persuader (je n'ai pas la prétention de démontrer quoi que ce soit) de l'existence de l'IDM ?

Il me semble que l'IDM, par définition, correspond à l'opposé/l'inverse/la réciproque (je ne suis pas très à l'aise avec ces notions) de la complexité de Kolmogorov.

Etant donné que l'IDM est l'information décompressée maximale, cela signifie que son programme le plus petit, c'est à dire l'information compressé (la séquence ADN si vous préférez) représente dans notre cas la complexité de Kolmogorov.

Plus l'ID d'un génome est proche/tend vers l'IDM, plus cela signifie que la séquence ADN correspondante est proche /tend vers la complexité de Kolmogorov.

Vous voyez donc que ces différents objets que je vous ai décrits, entretiennent des liens étranges avec les 3 théories de l'information: la séquence compressée (ADN) et l'IDM sont toutes les deux des chaines de caractères mesurables en bits (selon Shannon). Le passage de la séquence compressée à l'IDM se fait en faisant appel à la profondeur logique de Bennett mais le passage inverse est étrange car la séquence compressée, c'est par définition la complexité de Kolmogorov vis-à-vis de l'IDM.

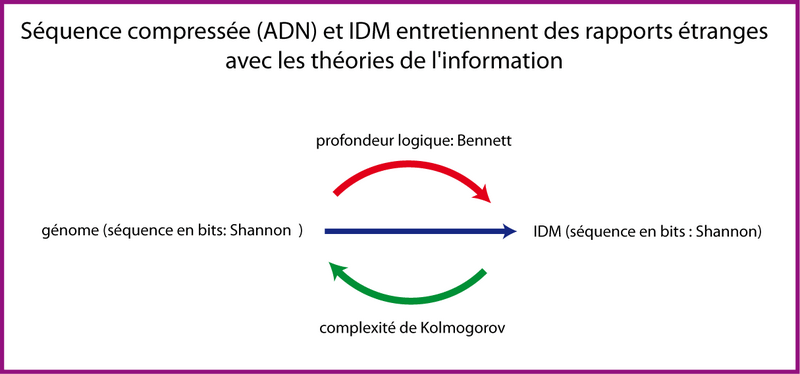
Or cela pose un problème. En effet, la fonction qui prend une séquence (IDM) en argument et renvoie la complexité de Kolmogorov (la séquence ADN compressée) est une fonction non calculable par une machine de Turing (un ordinateur) car, nous l'avons vu, elle est non récursive.

Je ne sais pas exactement ce qu'il en est de la fonction opposée prenant en argument la séquence compressée ADN et renvoyant l'IDM: est-elle calculable ? Car la profondeur logique, elle aussi, est non récursive.

A partir de là, il y a deux manières d'envisager les choses:

• Les biologistes vont se heurter à la théorie de la calculabilité. Nous ne pourrons peut-être jamais déterminer/mesurer l'ID ou l'IDM d'une séquence ADN en utilisant une fonction ni déterminer la séquence ADN à partir de l'ID ou l'IDM. Cela signifierait que l'objet que je ressens comme "mathématique" décrivant les interactions virtuelles entre nucléotides est soit inaccessible, soit inexistant. Ou en tout cas, il ne peut pas être "utilisé/traité" pour aboutir à la compression ou la décompression. Dans ce cas de figure, même la nature se heurte à la théorie de la calculabilité: l'ADN (l'immense compréhension de l'information) représenterait alors l'aboutissement de milliards d'années d'évolution, de milliards d'années de recherche de la séquence la plus courte possible étant donnée une ID dans le but de tendre vers la complexité de Kolmogorov.
• l'autre manière de voir les choses consiste à dire que le fonctionnement de la "nature" diffère d'une machine de Turing (d'un ordinateur) dans sa manière de compresser et décompresser l'information. Cette même nature est capable de "by-passer" la théorie de la calculabilité, elle peut compresser au maximum et décompresser au maximum une information de manière "pseudo-récursive" via un type de machine, de fonctionnement qui nous échappe.

A vrai dire, je penche plutôt pour le premier point, plus respectueux des paradigmes d'informatique et de biologie. Cependant j'ai le sentiment qu'à partir d'une séquence donnée, on devrait pouvoir connaitre la quantité d'information maximum injectable dans cette séquence car cette quantité ne me semble pas infinie. Or si on peut faire le chemin dans un sens via un objet mathématique, je ne vois pas de raison, à première vue, de ne pas pouvoir le faire dans l'autre sens ⁵ .

Voila, j'en ai terminé avec l'information. Vous l'aurez compris, je suis maintenant perdu en pleine jungle. Des aventuriers suivront-ils ma piste ? Ou flaireront-ils au contraire dés le départ qu'elle ne mène nulle part ? A vrai, dire, me reposant maintenant contre un arbre dans cette forêt vierge, je m'attends plutôt à ce que quelques singes rieurs se moquent gentiment de moi, ou qu'un boa vienne tordre le cou à mes allégations. Tel est le risque lorsque l'on s'aventure seul dans la jungle. Mais c'est un risque à prendre.

Bibliographie

1. Danchin, A. (2009). "Information of the chassis and information of the program in synthetic cells." Syst Synth Biol 3(1-4): 125-34.
2. [Rajout 2023] Jean-Paul Delahaye. Information, Complexité et Hasard. Notons qu'une grande part du début de ce chapitre (Shannon, Kolmogorov, Bennett) provient entre autre de la lecture de cet ouvrage de Jean-Paul Delahaye. Certaines idées personnelles (la découpe de l'ADN) me sont venues à la lecture de cet ouvrage mais par peur d'une mécompréhension de ma part, j'ai dû m'abstenir de citations précises par peur du contre-sens.

Notes de bas de pages

1. Antoine Danchin, La barque de Delphes, Odile Jacob.
2. Pour reprendre la formulation d'Antoine Danchin.
3. Antoine Danchin, Information of the chassis and information of the program in synthetic cells, Syst Synth Biol, 2009.
4. Site Web d'Antoine Danchin: www.normalesup.org/~adanchin/.
5. Il y a encore ici un risque de faiblesse du raisonnement mathématique (problème relatif aux notions d'injection/surjection?)