La modélisation d'un réseau de régulation

Préambule

Ce chapitre (et le chapitre qui suit sur les systèmes dynamiques) s'inspire de deux ouvrages que je conseille vivement: il s'agit de An introduction to systems biology (Uri Alon) et Computational modelling of gene regulatory networks: a Primer (Hamid Bolouri). J'ai écrit ce chapitre pour les biologistes qui souhaiteraient connaître les bases nécessaires à la modélisation d'un réseau de régulation génique simple. Je pense en particulier à des étudiants IGEM biologistes qui voudraient comprendre ce que font les étudiants IGEM informaticiens/mathématiciens. Ce chapitre décrira le fonctionnement de petits modèles d'équations différentielles ordinaires et leur implémentation sous Matlab. A la fin du chapitre, j'aborderai également une technique d'optimisation pour identifier des paramètres: l'algorithme génétique.

Pourquoi modéliser ?

On m'a souvent demandé à quoi servait la modélisation. Et parfois, je sentais bien que mon interlocuteur souhaitait plus m'imposer sa réponse à lui que d'écouter la mienne. En effet, beaucoup pensent que "modèle, c'est le mot à la mode à placer dans un projet de recherche pour avoir des sous". Dans ce chapitre, je vais tenter de démontrer aux sceptiques que la modélisation s'imposera inexorablement en biologie. Ceux qui pensent qu'il s'agit d'une mode sont, il me semble, dans l'erreur.

Raisonnons par l'absurde. Le sceptique envers la modélisation défend l'idée que pour décrire un système vivant, il faut décrire la structure et la fonction des composants ainsi que les interactions qui unissent ces composants en les représentant par des flèches. Ces flèches et la planche statique que le sceptique dessine sur une feuille de papier représentent, selon lui, le plus haut niveau de compréhension. Il pense aussi que le simple regard de ces planches ainsi que son intuition lui permet de déduire "mentalement" la dynamique du système. Malheureusement, cet objet mental est trop vite limité par nos capacités cognitives et ne remplit donc pas, c'est le moins qu'on puisse dire, le critère minimum d'objectivité requis par la méthode scientifique. Il devient alors nécessaire de faire appel à la modélisation mathématique pour dépasser les limites de notre intuition. Prouvons-le maintenant:

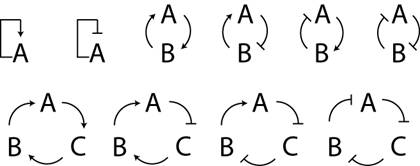
Figure 1. Les limites de l'intuition. Chaque petit réseau représente ce que j'appelle une planche statique. La connaissance des interactions ne suffit pas à prédire la dynamique de fonctionnement du réseau et sa fonction.

Parmi les petits réseaux ci-dessus, quels sont ceux qui permettent de générer des oscillations dans les concentrations des protéines (A, B, et C) ? Pas facile n'est ce pas ? On observe que même avec des réseaux très simples contenant seulement deux ou trois protéines, la présence de boucles de rétroaction positive ou négative complique très vite la tâche de l'intuition. Cette dernière ne peut tout simplement pas prédire la dynamique résultante de manière certaine. J'avoue ne pas savoir, moi-même, lesquels de ces réseaux sont capables de générer structurellement des oscillations. Une chose est sûre cependant: le dernier en est capable. Il s'appelle "le repressilator" et nous y reviendrons largement.

Alors pourquoi modéliser ? Dans ce chapitre, je montrerai deux exemples concrets qui illustrent l'intérêt de la modélisation. Nous verrons comment un modèle:

permet de dépasser les limites de l'intuition.
permet d'identifier des paramètres biologiques d'intérêt comme par exemple une constante de dissociation ou un taux de synthèse.

On peut ranger grossièrement les modèles en deux catégories: les modèles descriptifs qui fournissent un niveau de description bien plus poussé que ne le ferait une simple planche statique et les modèles prédictifs qui, comme leur nom l'indique, génèrent des prédictions que l'on peut ensuite évaluer/comparer avec des données expérimentales.

Imaginez une équipe de biologistes qui souhaiterait comprendre le fonctionnement d'un petit réseau de régulation comportant 20 protéines (20 gènes) chez une bactérie. L'équipe va peut être commencer par mesurer expérimentalement la concentration des 20 protéines dans une souche sauvage. Puis pour comprendre le fonctionnement dynamique du réseau, ils vont vouloir le perturber, par exemple en supprimant des gènes. Ils pourront facilement construire les 20 simples mutants mais construire les 190 doubles mutants, 1140 triples mutants etc...¹ sera déjà beaucoup plus fastidieux. Le nombre d'expériences que pourrait potentiellement faire l'expérimentaliste croît très rapidement, mais toutes ne sont pourtant pas aussi informatives. Un bon modèle permettrait par exemple de sélectionner les expériences les plus prometteuses (les doubles et triples mutants potentiellement intéressant à construire) parmi un grand nombre d'expériences possibles.

Il me faut cependant relativiser la portée de ces modèles prédictifs quitte à être critique. En effet, cet objectif de prédiction est souvent théorique car extrêmement difficile en pratique. Comme le souligne Antoine Danchin, on ne compte plus les modèles qui ont redécouvert le cycle de Krebs (Danchin 2009). En d'autres termes, les modèles actuels prédisent souvent ce que l'on connait déjà.

Le couple modèle--expérience est une démarche considérée comme saine qui est souvent mise en avant dans les projets de recherche. On retrouve le plan classique: développement d'un modèle parallèlement aux mesures expérimentales puis confrontation du modèle avec ces données expérimentales. Mais, en réalité, comme le souligne Antoine Coulon ² , "la confrontation [modèle--données expérimentales] est plus un processus qu'un moment donné dans le projet".

"La confrontation données--modèles n'a de sens que si elle est itérative sur une boucle courte, c'est-à-dire toutes les étapes (et tous les domaines de compétence) sont susceptibles de se fertiliser mutuellement."

Ainsi, il me semble que la confrontation du modèle prédictif avec les données expérimentales a souvent pour objectif idéaliste de faire émerger:

des prédictions vérifiées expérimentalement et donc un modèle "vrai" (or un modèle est faux par définition)
une grande quantité d'information "intelligible" extraite des données expérimentales grâce au modèle.

Dans la pratique, je pense que cet objectif idéaliste est assez rarement atteint mais cela n'est pas un problème. Je pense que l'apport principal du couple modèle--expérience n'est pas toujours là où on l'attend. Son but officieux/sa conséquence pratique est de créer un couple modélisateur--expérimentateur partageant deux savoirs distincts dans le but d'envisager la biologie sous le prisme des systèmes dynamiques et de la complexité. Mathématiciens et biologistes s'influencent mutuellement et apprennent à créer puis partager un savoir commun. Ainsi, l'intérêt principal de la modélisation est d'influencer la manière dont le biologiste pense, travaille et donc "design" ses expériences. Un bon modèle n'a pas pour unique but de générer des prédictions ou d'extraire des informations des données expérimentales: un bon modèle change l'expérience elle-même en changeant le regard de l'expérimentateur.

Aujourd'hui, un biologiste n'envisage plus raisonnablement de travailler sans ordinateur, sans internet, Word ou Excel. Dans quelques années, la complexité des données sera telle que le biologiste ne pourra plus raisonnablement faire de la biologie sans taper une ligne de code. Les langages de programmation (R, Matlab, Python...) changeront durablement sa manière de travailler, de penser ses expériences. Les mots complexité--modèle--système dynamique lui apparaitront moins mystérieux et donc moins suspects.

Petit encouragement au biologiste réfractaire

Le chapitre qui suit est riche en équations. Cependant, je souhaite tout de suite rassurer le lecteur biologiste potentiellement allergique aux mathématiques. Ce qui suit est écrit spécialement pour lui et ne dépassera jamais le niveau de terminale scientifique: c'est-à-dire mon propre niveau. Il me faut cependant introduire deux concepts barbares: "équation différentielle" qui, dans mon exposé, ne signifiera jamais autre chose que "taux" et "matrice" qui ne signifiera jamais plus que "tableau de nombres".

Le biologiste devrait considérer la suite comme des travaux pratiques de mathématiques expérimentales. L'intérêt principal consiste à jouer "empiriquement" avec les systèmes dynamiques et cela est rendu possible par l'utilisation des méthodes numériques. Ce qui est important c'est d'étudier, de comprendre et de "jongler" avec le code: essayer par exemple de remplacer par un "3" la valeur numérique d'un paramètre fixé initialement à "5" puis regarder "la conséquence" sur les profils dynamiques. Le but est de "ressentir" de l'intérieur le système et la méthode. Un petit peu comme une expérience de biologie que l'on répète 100 fois de suite jusqu'à presque "ressentir" ce qui se passe dans le tube. La plupart des figures présentes dans ce chapitre ont été créées avec un script (un programme court) écrit avec le langage "Matlab". Chaque script est accessible facilement (suivant le support sur lequel vous lisez cette thèse: Web/papier). J'ai essayé de commenter mon code au maximum pour rendre facile sa compréhension. Cependant, il est impossible de tout expliquer et un effort restera toujours nécessaire pour comprendre la logique des scripts, pour rentrer dans la tête du programmeur. J'ai choisi d'utiliser MATLAB qui est à la fois un langage de programmation et un environnement de développement. Son inconvénient c'est qu'il est payant et non libre. Son avantage c'est qu'il existe une multitude de fonctions et "toolbox" déjà codées qui évitent de réinventer la poudre. Mais son plus gros avantage selon moi, c'est l'aide très complète et les nombreux didacticiels très bien construits qui permettent de faire ses premiers pas "en douceur". Et cela est particulièrement important quand on n'a pas la culture de l'informatique. Avec un outil comme Matlab, vous pouvez faire, par exemple, du traitement d'image/de vidéo, vous pourrez également faire de la bioinformatique, des simulations de systèmes biologiques, du traitement de données lourd ou générer des figures complexes pour une publication. Bien sûr, vous disposez d'une multitude d'autres outils à peine plus complexes et à la fois utiles et amusants comme des outils d'optimisation (algorithme génétique) ou des algorithmes d'apprentissage (réseaux de neurones). Bon, j'en ai terminé avec la publicité. Sachez qu'il existe aussi des équivalents libres comme Scilab ou Octave ou même d'autres langages tout aussi intéressants comme Python ou R. On peut également espérer que, d'ici quelques années, apparaissent des environnements de développement intégrés (IDE) spécifiques à la biologie synthétique/des systèmes.

La section qui suit "quelques conjectures nécessaires" est un petit peu difficile et est donc plutôt destinée à des experts. Cependant, sa compréhension n'est absolument pas indispensable pour la suite de mon exposé qui sera, elle, plus abordable.

Quelques conjectures nécessaires

Ce chapitre introduit l'utilisation d'un formalisme mathématique adapté pour modéliser la dynamique de fonctionnement d'un réseau de régulation génique en considérant le comportement moyen d'une population de cellules génétiquement identiques. Ce formalisme est basé sur la loi d'action des masses et nous permettra d'introduire l'utilisation des équations différentielles ordinaires (ODE). Cependant, avant de rentrer dans le vif du sujet, je souhaiterais aborder ce que ce formalisme ne modélisera pas. Autrement dit, je souhaiterais insister sur les hypothèses initiales (assumptions en anglais) sur lesquelles repose la suite. Que se passe-t-il donc "pour de vrai" dans une cellule que nos modèles ne montreront pas?

Processus stochastiques basés sur des réactions chimiques

Ce chapitre décrit la modélisation ODE basée sur la loi d'action des masses. Ce formalisme est particulièrement bien adapté lorsqu'il s'agit de comparer les résultats issus de simulation avec ceux issus des expériences. En effet, la plupart des mesures des concentrations cellulaires d'ARN ou de protéines sont effectuées à partir d'extraits issus d'un grand nombre de cellules (une population). Les résultats obtenus à partir de ces extraits représentent une moyenne apportant une information sur le comportement moyen d'une cellule. Or cette moyenne cache la variabilité qui existe entre les cellules. Cette variabilité intercellulaire est due aux déplacements aléatoires des molécules selon le mouvement brownien. Cela injecte des probabilités dans les phénomènes observés. Probabilités qu'il est nécessaire de prendre en compte si l'on veut décrire ce qui se passe dans une cellule unique mais que l'on peut ignorer si on regarde le phénomène à l'échelle de la population. Nous reviendrons plus tard sur les méthodes de modélisation stochastique de l'expression des gènes. Cependant rappelons brièvement ici que la fréquence des collisions est fonction de la concentration des molécules et de leurs vitesses. Parmi toutes les collisions, seule une partie des molécules ont une énergie suffisante et la bonne orientation au moment de l'impact pour rompre les liaisons existantes et en former de nouvelles. L'énergie thermique minimale pour dépasser la barrière de transition permettant à la réaction chimique de se produire s'appelle l'énergie d'activation. Une des caractéristiques importantes de la biochimie cellulaire c'est que cette barrière d'énergie n'est pas suffisamment haute pour empêcher les changements aléatoires d'état aux températures physiologiques. Ceci signifie que la plupart des interactions protéines--protéines et ADN--protéines sont constamment en train de se former puis de se dissocier.

Homogénéité du milieu, diffusion et encombrement

Dans les modèles ODE que nous allons étudier, nous allons parler de concentration de protéines. Ces concentrations seront toujours considérées comme homogènes dans la cellule E. coli. Nous ne modéliserons pas l'espace et il n'y aura donc pas de gradient spatial. Bien que, contrairement aux cellules eucaryotes, il n'y ait pas de compartiments chez E. coli, cela n'empêche pas l'existence de ces gradient spatiaux (Llopis et al.). De plus, l'espace dans la cellule est extrêmement encombré ce qui réduit significativement les taux de diffusion des protéines et des complexes macromoléculaires (Zhou et al. 2008) (Elowitz et al. 1999). Une des conséquences directe est la ségrégation des molécules qui ont une affinité les unes pour les autres ce qui crée des concentrations locales plus fortes. Pour l'interaction ADN--protéine, il a été montré que l'effet de l'encombrement peut augmenter l'activité de la liaison ADN--protéine par plus d'un ordre de grandeur (Poon et al. 1997).

Recherche du site de liaison sur l'ADN par le facteur de transcription

On sait depuis les années 70 que les facteurs de transcription trouvent leur site de liaison beaucoup plus vite que ce qui serait attendu avec une diffusion simple en 3 dimensions (Riggs et al. 1970). L'hypothèse actuelle propose une recherche avec deux types de diffusion (von Hippel and Berg 1989). Le facteur de transcription recherche sa cible (son site de liaison) par glissement le long d'un court segment d'ADN (~100pb). Cela représente une diffusion facilitée à 1 dimension. Puis le facteur de transcription se dissocie, diffuse dans le cytoplasme (en 3 dimensions) avant de se lier à une nouvelle région d'ADN sur lequel il glisse à nouveau. La protéine ne restant sur l'ADN que quelques millisecondes, ce processus peut être itéré un grand nombre de fois jusqu'à ce qu'elle trouve enfin sa cible (en moins de 5 minutes) (Elf et al. 2007; Li and Elf 2009). Selon ce modèle de recherche, il est possible que notre vision binaire de la liaison ADN--protéine (faible--forte /spécifique--aspécifique) soit fausse et qu'il soit plus réaliste de penser en terme de "gaussienne" des distributions d'affinité des sites de liaison pour un facteur de transcription donné (Slutsky and Mirny 2004).

Transcription et traduction

Dans les modèles que nous allons décrire, la machinerie globale (ARN polymérase, ribosomes) et l'énergie (ATP, pouvoir réducteur) seront toujours considérés en excès et donc non limitants. De plus, le délai de transcription--traduction--repliement qui existe entre la fixation du facteur de transcription activateur et l'arrivée des premières protéines fonctionnelles ne sera pas pris en compte.

Approximation pour les réactions rapides

Les régulations allostériques (fixation de l'IPTG sur le répresseur LacI par exemple), modifications post traductionnelles (phosphorylation, acétylation..) et les réactions métaboliques s'effectuent à une vitesse très rapide (millisecondes, secondes). Par conséquent, elles sont considérées "à l'équilibre" par rapport aux régulations géniques (minutes, heures). Autrement dit, l'ajout d'IPTG en concentration suffisante dans le milieu change instantanément l'affinité de LacI pour l'ADN par rapport à l'arrivée de la β-galactosidases. Il n'est donc pas nécessaire de modéliser explicitement l'import de l'IPTG et la formation du complexe [lacI.IPTG] en fonction du temps.

Intégration des signaux au niveau des promoteurs complexes

Nos modèles représentent toujours des cas simples avec soit 1, soit 2 facteurs de transcriptions régulant l'activité d'un même promoteur. Lorsque ces deux facteurs sont présents en même temps, on utilise la logique booléenne classique (fonction AND ou OR par exemple) pour intégrer le signal résultant. Mais comment intégrer les signaux issus de promoteurs plus complexes comme le promoteur aceBAK ci-dessous ? Quelle allure a la fonction de sortie qui décrit l'activité d'un promoteur complexe en fonction de ses "entrées" protéiques? On touche ici à deux limitations:

une limitation expérimentale: aucune méthode n'est en mesure actuellement de fournir une résolution suffisante pour nous aider à déterminer cette fonction.
une limitation relative au formalisme de modélisation: de mon point de vue, seul un modèle spatial à l'échelle de l'atome et de la liaison chimique peut fournir la fonction qui décrit l'activité d'un promoteur complexe en fonction de ses "entrée" protéiques.

Promoteur de l'operon aceBAK — Figure 2. La régulation très complexe de l'operon aceBAK (image Ecocyc).

La topologie du réseau est dynamique

Dans les modèles que nous allons voir, la topologie sera considérée comme statique. En réalité, la topologie est dynamique et devrait, dans l'absolu, être modélisée comme une variable. Par exemple, les variations de super-enroulement (qu'on appelle aussi topologie mais qui n'a rien à voir avec la topologie dont je parle ici) de l'ADN peuvent supprimer l'affinité d'une protéine pour un site sur l'ADN ce qui supprime l'existence de cette interaction.

Le formalisme des équations différentielles

Quel est le point de départ du biologiste qui souhaite modéliser la dynamique de fonctionnement d'un réseau de régulation génique? Le biologiste veut suivre l'évolution de la concentration d'une protéine en fonction du temps.

Le nombre de protéines B dans une bactérie au temps t+dt est égal au nombre de protéines B au temps t auquel on ajoute la quantité synthétisée κ.dt durant le temps dt et auquel on soustrait la quantité dégradée γ.dt.[B] durant le temps dt. Comme le volume de la bactérie est considérée constant, notez également que l'on peut aisément passer du nombre de molécules aux concentrations et vice versa en divisant ou en multipliant par le volume.

On a:

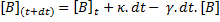
Je vois venir votre question: pourquoi la quantité dégradée est-elle proportionnelle à B ? Cela est dû aux "histoires de demi-vie" dont je suis sûr qu'il vous reste surement quelques traces: la fonction qui décrit cette dégradation est une exponentielle et non une droite. Par exemple si la synthèse s'arrête (κ=0) et qu'on a ɣ=1/2, dt=1 et B=100 au temps t, alors à t+1, B=50 et on a dégradé 50 molécules de B. A t+2, B=25 et on a dégradé 25 molécules de B, à t+3, B=12.5 et on a dégradé 12.5 molécules de B. On voit donc bien que le nombre de molécules de B dégradées dépend du nombre de molécules de B déjà présentes. Vous pouvez aussi constater, en fronçant les sourcils sur le "12.5 molécules de B", l'intérêt de travailler en concentration (nombre réel, continu) et non en nombre de molécules (nombre entier, discret).

Si on passe B de l'autre coté, on a:

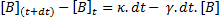
Si on divise les deux cotés par dt, on a:

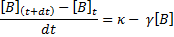
La voici donc notre première équation différentielle. Le taux de changement de la concentration de la protéine B par unité de temps (d[B]/dt) est proportionnel au taux de synthèse κ de la protéine B (qui inclut transcription et traduction) moins le taux de dégradation γ multiplié par [B].

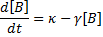
Le terme γ comprend à la fois la dégradation spontanée de la protéine et le taux de dilution. Ce dernier dilue le contenu protéique par deux à chaque fois que la cellule bactérienne se divise.

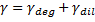
Suivant les conditions et l'organisme utilisé, c'est l'un ou l'autre de ces termes qui est prédominant. Par exemple, dans une cellule différenciée qui ne se divise plus ou alors pour des bactéries en phase stationnaires, on a 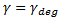equation . A l'inverse, pour des bactéries en phase exponentielle .

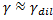Par définition, à l'état d'équilibre, on a 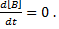equation Par conséquent, la concentration de B est constante. On déduit que [B] est égale au ratio entre les taux de synthèse et de dégradation.

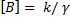
Petit détour par la loi d'action des masses

Maintenant, on sait suivre l'évolution de la concentration d'une protéine B en fonction du temps. Et ce qu'on voudrait c'est pouvoir moduler cette concentration en fonction du contrôle de la transcription du gène b. On peut donc souhaiter qu'un gène b soit activé par un facteur de transcription A.

Figure 3. Schéma d'une activation transcriptionnelle simple.

Ainsi, si la protéine A se fixe au promoteur du gène b, cela facilite le recrutement de l'ARN polymérase qui transcrit le gène b. L'ARN correspondant est ensuite traduit ce qui résulte en une accumulation de la protéine B. C'est donc le taux de synthèse de la protéine B qui est fonction de la concentration du facteur de transcription A tel que:

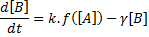
Mais quelle est cette fonction f ? Cette fonction relie la concentration moyenne du facteur de transcription A au niveau moyen d'ARN et de protéines B produites. Elle correspond à la fraction de cellules dont le promoteur du gène b (ADN) est occupé par le facteur de transcription A (et donc permettant l'initiation de la transcription) parmi toutes les cellules (et donc tous les promoteurs). Autrement dit c'est la fraction de complexe (ADN--protéine A) parmi tout les sites d'ADN libre. Cette fraction correspond à la probabilité que le promoteur soit actif. Ainsi le site ADN peut être soit fixé à la protéine A soit libre ce qui résulte dans l'équation de conservation suivante:

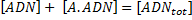
où ADN_tot est la concentration totale de sites cibles d'ADN (promoteurs du gène b dans une population de cellules). Les protéines A (notées A) et le promoteur (noté ADN) diffusent dans le cytoplasme et occasionnellement se rencontrent pour former le complexe [A.ADN]. Ce processus est décrit par la cinétique d'action des masses où A et ADN entrent en collision et se lient à un taux k_on. Le taux de formation du complexe est proportionnel au taux de collision, donné par le produit des concentrations A et ADN:

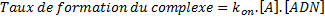
Le complexe [A.ADN] peut se dissocier à un taux k_off . Le taux de changement de [A.ADN] basé sur ces processus de collision et de dissociation est décrit par la cinétique d'action des masses:

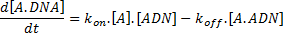
A l'état d'équilibre (d[A.DNA]/dt=0), on a:

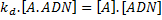
Où k_d représente la constante de dissociation 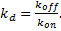Ainsi la fraction d'ADN sur lequel A est lié est:

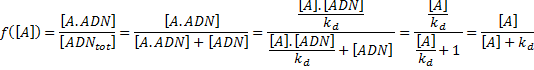
Cette équation correspond à l'équation de Michaelis et Menten plus connue dans le contexte de la cinétique enzymatique.

Si on remplace f(A) dans l'équation mentionnant f(A) un peu plus haut, on obtient:

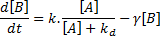
C'est cette première équation que nous allons écrire puis "intégrer" dans "Matlab".

Etude du code

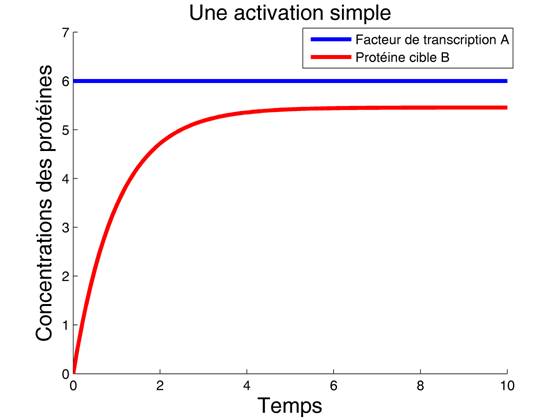
Vous pouvez copier le code présent ci-dessous puis aller dans Matlab, File, New, Blank m-file et coller le code. Appuyer sur F5 pour exécuter le code. La figure 4 apparait. On observe que la concentration du facteur de transcription A est constante. Celui-ci active la transcription du gène b ce qui augmente transitoirement la concentration de la protéine B. Puis cette dernière atteint un état d'équilibre. On peut donc découper la régulation en deux états. Un état transitoire d'adaptation et un état d'équilibre (steady state en anglais) lorsque les concentrations deviennent constantes.

Figure 4. Dynamique d'une activation simple. Voir le code Matlab ci-dessous qui gènère cette figure.

Cliquer pour voir le code Matlab

                
function ActivationSimple
% tout ce qui est en vert (derrière le pourcentage sont des commentaires
% qui ne sont pas "interprétés".
% on crée une fonction qui contient les equations. 
function dydt = equations(t,y)    
% crée une matrice de deux ligne et une colonne qu'avec des zeros 
% la ligne 1 concentration de A c'est y(1) et ligne 2 celle de B c'est y(2)
    dydt=zeros(2,1);
% on considère la concentration de A constante donc sa derivée est nulle    
    dydt(1) = 0;
% la fameuse equation   
    dydt(2) = kappa*(y(1)/(kd+y(1)))- gamma*y(2);
end
% on fixe une valeur numerique à nos trois paramètres
kappa=10;
kd=5;
gamma=1;
%y0 c'est le vecteur (=matrice à une ligne) correspondant aux conditions
%initiales. A est à une concentration initiale relative de "6" et B a une
%concentration initiale nulle.
y0=[6, 0];
% fixe les options du solveur numerique. les concentrations ne peuvent pas
% être négative
Options = odeset('NonNegative',[1,2]);
%Vecteur Temps qui va de 0 à 10 par petit pas de 0.1
Time=[0:0.1:10];
% utilise un solveur numerique qui "integre" les equations. Nous
% biologistes nous moquons de comment se solveur fonctionne: il fait le job
% c'est tout. ceux qui veulent plus de detail peuvent taper méthode de
% rugge kutta sur wikipedia. A partir de dydt de la fonction equation, le
% solveur nous renvoie y en fonction de t etant donné la condition initiale
% et les options
[t,y]=ode45(@equations,Time,y0, Options);

% crée une nouvelle figure matlab dans laquel on plot les resultats
figure('Color', 'w')
hold on % permet de superposer les courbes

% trace l'evolution de la concentration de A en fonction du temps
plot(t, y(:,1),'-b','LineWidth',3)
% trace l'evolution de la concentration de B en fonction du temps
plot(t, y(:,2),'-r','LineWidth',3)
% annotation des axes, titre et legende
axis([0 10 0 7])
xlabel('Temps','FontSize',16)
ylabel('Concentrations des protéines','FontSize',16)
title('Une activation simple','FontSize',16)
legend('Facteur de transcription A','Protéine cible B');
end

Le code peut sembler compliqué à première vue mais sachez que tout ce qui est en vert c'est les commentaires (les explications). Ce code peut être découpé en plusieurs parties:

La fonction nommée "équation" décrit le système composé de deux équations différentielles. La première équation représente l'évolution de la concentration du facteur de transcription A en fonction du temps (constante et donc nulle). La deuxième équation représente l'évolution de la concentration de la protéine B en fonction du temps et qui dépend de A.
L'attribution (arbitraire) de valeurs numériques aux 3 paramètres (κ, γ, kd) ainsi que les deux conditions initiales qui correspondent aux concentrations de A et de B au temps t=0. Notez que dans tous les scripts que nous allons étudier, j'attribue toujours une valeur arbitraire aux paramètres. Les modélisateurs plus sérieux recherchent dans la littérature si les valeurs numériques des paramètres ont été identifiées ou à défaut, ils les fixent à des valeurs biologiquement raisonnables.
L'intégration de la fonction "équation" est faite par un solveur numérique: c'est une fonction de Matlab appelée ode45 qui intègre "numériquement" l'équation différentielle c'est-à-dire qu'elle calcule l'évolution de la concentration de A et B en procédant par itération successive. A chaque petit pas, le solveur fait une petite erreur (négligeable pour nous) et la solution proposée n'est donc pas exacte. Pour avoir une solution exacte, il faudrait intégrer "analytiquement" l'équation mais cela s'avère en général impossible pour des systèmes d'équations non linéaires trop complexes.
La fonction ode45 renvoie comme par magie les concentrations de A et de B (stockées en ligne dans la matrice y) en fonction du temps. On peut ensuite tracer les résultats dans la figure et ajouter un titre, une légende et des noms aux axes.

Cas du répresseur

Dans le cas où A réprime B, on montre facilement que:

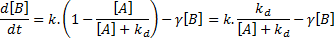
Cas de l'inducteur allostérique

Il arrive très souvent qu'un facteur de transcription soit activé par un inducteur. C'est le cas, comme nous l'avons vu, de la protéine Crp qui est spécifiquement activée par la petite molécule AMP cyclique. La liaison de l'AMPc à Crp change sa conformation et augmente son affinité pour son site spécifique sur l'ADN. L'échelle de temps de la fixation de l'AMPc à Crp est beaucoup plus courte que celle des processus de régulation génique. Nous faisons donc l'approximation du quasi état d'équilibre (quasi steady state). Dans le cas simple sans coopérativité, on a:

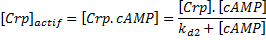
où k_d2 est la constante de dissociation de l'AMPc à Crp.

Dans le cas de la protéine Acs, sur laquelle j'ai travaillé, et dont la transcription est spécifiquement activée par le complexe [Crp.cAMP], le taux de changement de sa concentration s'écrit donc:

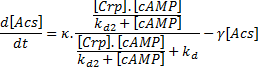
où k_d est la constante de dissociation du complexe Crp--cAMP à l'ADN.

Voici la figure que l'on obtient cette fois. Remarquez que sans les commentaires, le code est beaucoup plus court.

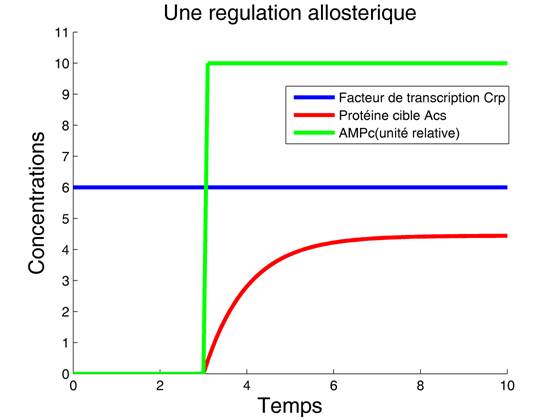
Figure 5. Dynamique d'une régulation allostérique. Voir le code Matlab ci-dessous qui gènère cette figure.

Cliquer pour voir le code Matlab

                
function RegulationAllosterique
function dydt = equations(t,y)
dydt=zeros(2,1);
AMPc=kappa*(t>T_AMPc); 
dydt(1) = 0;
dydt(2) = kappa*(y(1)*AMPc)/(kd2+AMPc)/(kd+(y(1)*AMPc)/(kd2+AMPc))- gamma*y(2);
end
kappa=10;
kd=5;
kd2=5;
gamma=1;
T_AMPc=3;
y0=[6, 0];
Options = odeset('NonNegative',[1,2]);
Time=[0:0.1:10];
[t,y]=ode45(@equations,Time,y0, Options);
figure('Color', 'w')
hold on
plot(t, y(:,1),'-b','LineWidth',3)
plot(t, y(:,2),'-r','LineWidth',3)
plot(t, kappa*(t>T_AMPc),'-g','LineWidth',3);
xlabel('Temps','FontSize',16)
axis([0 10 0 11])
ylabel('Concentrations','FontSize',16)
title('Une regulation allosterique','FontSize',16)
legend('Facteur de transcription Crp','Protéine cible Acs','AMPc(unité relative)');
end

Découplage de la transcription et de la traduction

Jusqu'à présent, nous avons fait l'hypothèse que le taux de synthèse incluait transcription et traduction. Il est bien sûr possible de découpler ces deux processus en deux équations différentielles distinctes pour, par exemple, y inclure des régulations traductionnelles. On a:

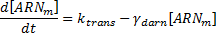
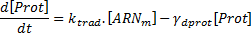
où κ_trans correspond au taux de transcription, γ_darn correspond au taux de dégradation des ARNm, κ_trad correspond au taux de traduction des ARNm et γ_dprot correspond au taux de dégradation de la protéine.

Cas de la liaison coopérative:

Il arrive parfois que la liaison du facteur de transcription au promoteur soit coopérative. Cela signifie qu'il faut plusieurs facteurs de transcription fixés au promoteur pour obtenir une activation complète de la transcription du gène B et que la fixation des premiers aide à la fixation des suivants. Quand tel est le cas, on utilise l'équation de Hill qui est un cas général de l'équation de Michaelis et Menten:

Figure 6. Liaison coopérative et fonction de Hill. Voir le code Matlab ci-dessous qui gènère cette figure.

Cliquer pour voir le code Matlab

                
function ParametreHill
% l'objectif de cette figure est de montrer coment varie B en fonction de
% l'activateur A quand on fait varier le paramètre de cooperativité n
figure('Color', 'w')
hold on
    function dydt = equations(t,y)
        dydt=zeros(2,1);
        dydt(1) = 0;
        % on ajoute le paramètre de hill n 
        dydt(2) = kappa*(y(1).^n/(kd.^n+y(1).^n))- gamma*y(2);
    end
% deux vecteurs qui sont "initialiser"
Y1=[];
Y2=[];
% on fait une boucle for pour tester differents paramètres n
for n=[1,2,4,10,20,300]
    kappa=10;
    kd=5;
    gamma=1;   
% on fixe la protéine B et on fait varier la concentration initiale de A 
% avec une nouvelle boucle for
    yo(2)=0;
    for i=1:0.2:10    
        yo(1)=i;
        Options = odeset('NonNegative',[1,2]);
        Time=[0:0.1:10];
        [t,y]=ode45(@equations,Time,yo, Options);
    % concatenation  dansun vecteur de la valeur finale de B quand on fait
    % varier la condition initale A
        Y1=[Y1 y(end,1)];
        Y2=[Y2 y(end,2)];  

        if i==10
            plot(Y1, Y2,'LineWidth',3,'color',[rand(1) rand(1) rand(1)]);    
            Y1=[];% delete le vecteur avant le changement de n
            Y2=[];   
        end    
    end
end
xlabel('Protéine A','FontSize',16);
ylabel('Protéine B','FontSize',16);
title('Variation du paramètre de hill','FontSize',16);
legend('n=1','n=2','n=4','n=10','n=20','n=300');
end

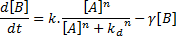
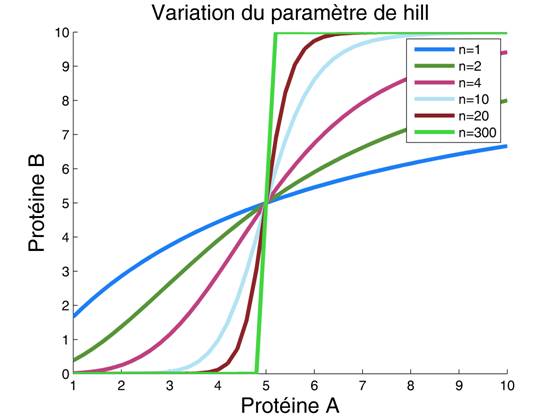
Cette équation introduit le paramètre de Hill noté n qui permet de contrôler l'allure et la pente de la courbe correspondante. Lorsque n=1, on obtient l'équation de Michaelis et Menten. Quand n augmente, la courbe devient sigmoïdale jusqu'à devenir une fonction en forme d'escalier lorsque n tend vers l'infini. On obtient alors l'équation linéaire par morceau ci-dessous.

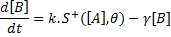
où S⁺ est une fonction en escalier et θ est une valeur seuil de telle manière que S⁺= 0 si [A]< θ et S⁺ = 1 si [A]> θ.

Ce formalisme booléen a été introduit par Leon Glass et Stuart Kauffman (Glass and Kauffman 1973) dans les années 70. Son principal avantage, c'est le peu de paramètres nécessaires (3 dans l'exemple ci-dessus) et cela a son importance étant donné le peu d'informations quantitatives généralement présentes dans la littérature. Notre laboratoire a participé à l'élaboration d'un logiciel librement accessible nommé Genetic Network Analyzer (GNA) basé sur ce formalisme booléen. Ce logiciel permet d'étudier qualitativement la dynamique de réseaux géniques de plus grosses tailles (de Jong et al. 2003). Il a été utilisé à plusieurs reprises avec succès pour modéliser des réseaux biologiques réels (Ropers et al. 2006).

Figure 7. Interface graphique (GUI) du logiciel Genetic Network Analyzer

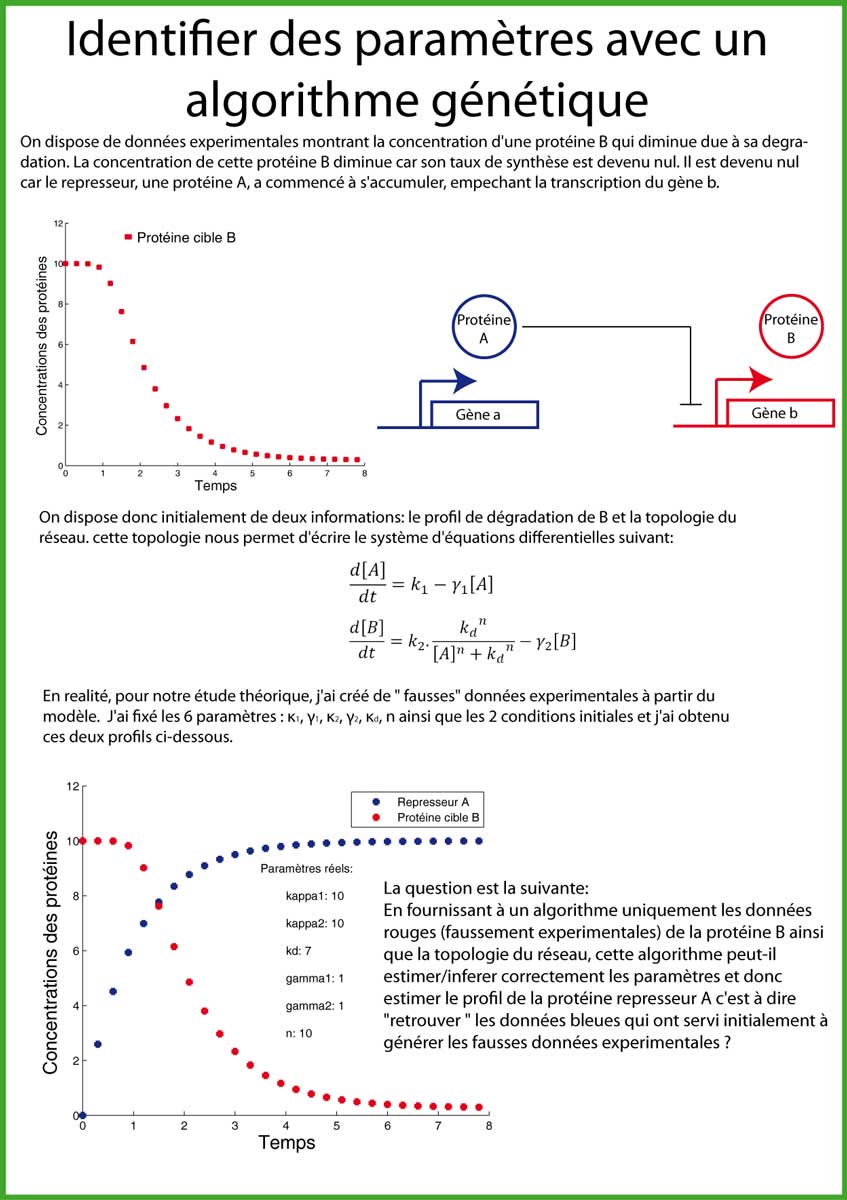
Identification de paramètres à l'aide d'un algorithme génétique

Imaginons que l'on ait acquis des données expérimentales montrant la dégradation d'une protéine B au cours du temps (voir la figure 8 pour bien comprendre le système). On sait également que la diminution de la concentration de la protéine B est due à l'arrêt de sa synthèse. Cet arrêt est lui-même lié à l'accumulation d'un facteur de transcription A qui réprime la transcription du gène b. La topologie (une répression simple) de notre réseau est donc connue. On peut modéliser la dynamique de fonctionnement de ce réseau à l'aide du système d'équations différentielles ci-dessous.

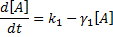
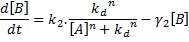
Il y a 6 paramètres inconnus: κ₁, γ₁, γ₂, κ₂, n et k_d.

L'objectif sera d'identifier/déterminer ces paramètres ce qui permettra également d'inférer la concentration du facteur de transcription A au cours du temps.

Plus exactement, mon but sera de vous prouver que l'on peut extraire beaucoup d'informations à partir d'un jeu de données limité. Et pour cela, je vais commencer par créer un faux jeu de données expérimentales à partir du modèle lui-même. Je fixe donc la valeur de 6 paramètres de manière arbitraire: κ₁=10, γ₁=1, κ₂=10, γ₂=1, k_d=7 et n=10 puis je génère les profils des protéines B et A en fonction du temps à l'aide des équations. Pour renforcer leur image de "données expérimentales", j'ai échantillonné ces courbes en 34 mesures temporelles (approximativement 4 points par unité de temps).

L'objectif est le suivant: on souhaite écrire un algorithme capable de "retrouver" ces 6 paramètres et retrouver également les données en bleu (la concentration du facteur de transcription A au cours du temps) uniquement à partir des données expérimentales en rouge ainsi que de la connaissance de la topologie du réseau.

Identification de paramètres — Figure 8. Identifier plusieurs paramètres à partir de données expérimentales et la connaissance de la topologie du réseau.

Retrouver/rechercher la valeur de ces paramètres consiste à résoudre un problème d'optimisation. Au début, on intègre notre système d'équations différentielles avec des paramètres choisis aléatoirement (souvent dans une fourchette biologiquement raisonnable, par exemple les réels positifs). Puis on compare la courbe proposée par le modèle décrivant [B] en fonction du temps avec le jeu de données expérimentales. Pour cela, on évalue la fonction proposée par le modèle aux 34 valeurs (n) de temps correspondant à l'échantillonnage des données expérimentales 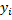equation ce qui génère un vecteur de même taille 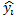. Puis on utilise la méthode des moindres carrés.

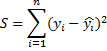
L'idée consiste ensuite à minimiser la valeur obtenue S. En effet, plus la valeur de S est petite, plus cela signifie que la courbe du modèle s'ajuste aux données expérimentales.

Un algorithme possible consiste à faire varier aléatoirement (avec la fonction rand de Matlab par exemple) les 6 paramètres que nous recherchons puis sélectionner le jeu de paramètres générant la plus petite valeur de S. Cependant, il est impossible de tester toutes les combinaisons et nous ne pourrons jamais savoir si nous avons vraiment trouvé la valeur minimum de S.

D'autres algorithmes utilisent l'information sur la dérivée pour trouver le minimum. Par exemple, si en augmentant tel paramètre, S diminue (sa dérivé est négative) alors l'algorithme continue à augmenter le paramètre jusqu'à ce que la dérivée devienne nulle. Au contraire, si S augmente (sa dérivé est positive), alors l'algorithme fait varier le paramètre dans l'autre sens. Mais ce type d'algorithme tombe très vite dans un minimum "local", c'est-à-dire un creux du paysage des paramètres qui n'est pas le minimum global recherché même si la dérivée est devenue nulle.

Ce dont nous avons besoin, c'est d'un algorithme qui fouille le "paysage" des paramètres de manière plus efficace qu'une recherche strictement aléatoire et qui est en même temps capable de s'échapper d'un minimum local (figure 9). Au fur et à mesure des itérations et en un temps raisonnable, l'algorithme doit nous fournir une solution qui s'approche du minimum global même si elle ne l'atteint pas. Un des algorithmes répondant à ce cahier des charges est l'algorithme génétique.

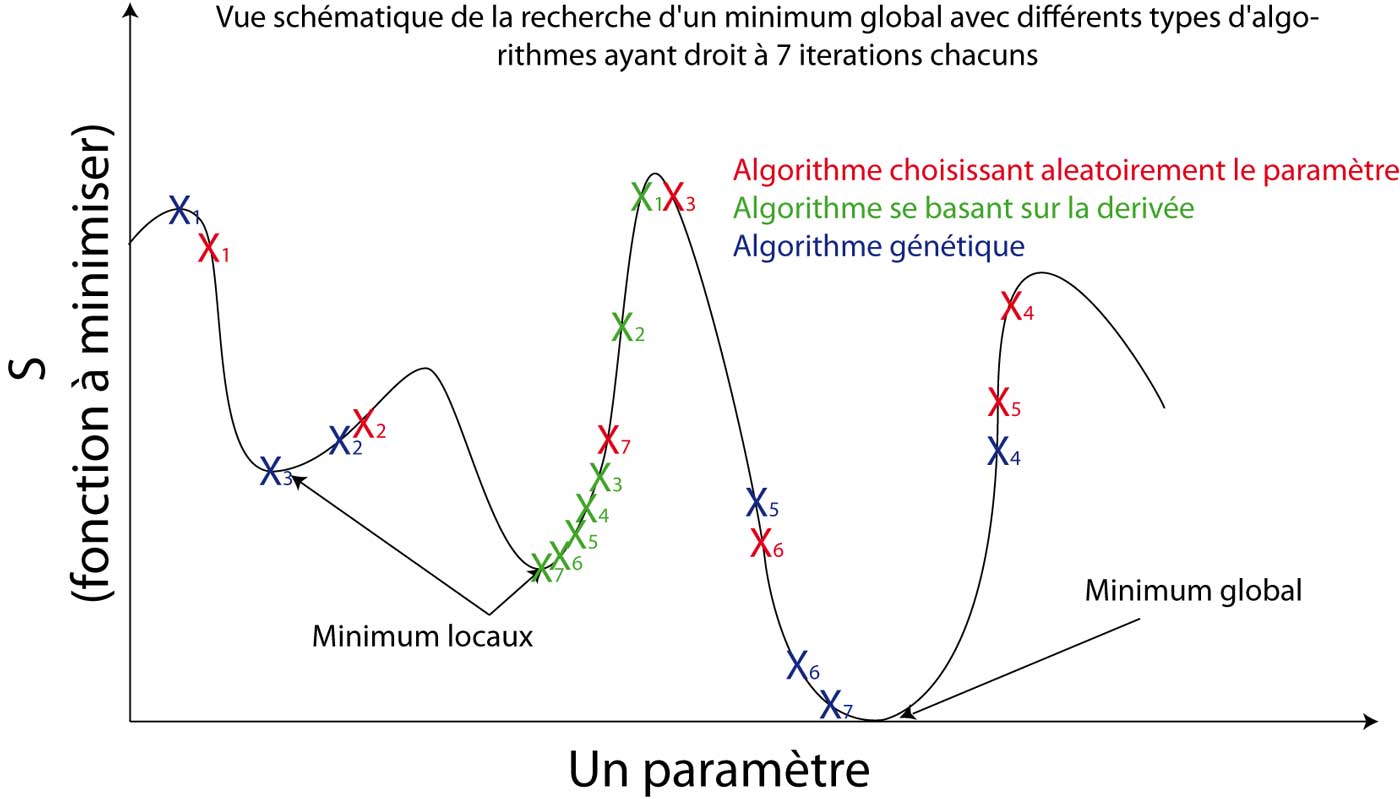
Figure 9. Schéma de la recherche d'un minimum global.

Les premiers algorithmes génétiques ont été développés par John Holland dans les années 60 (Holland 1975). Pour faire simple, un algorithme génétique met en compétition une population d'individus ayant chacun un jeu de paramètres. Le fitness des "individus" c'est-à-dire leurs capacités à se reproduire est fonction de la valeur de S. Dans notre cas (minimisation), les individus qui ont une faible valeur de S se reproduisent plus que ceux qui ont une forte valeur de S. A chaque cycle de reproduction, des mutations ont lieu pour fouiller l'espace des paramètres et s'échapper des minima locaux. Des recombinaisons (entre paramètres) (appelées aussi crossing-over) ont également lieu pour tenter de "mettre ensemble" de bons paramètres. Puis une sélection est mise en place pour limiter le nombre d'individus (très vite "computationnellement" couteux) en éliminant les plus faibles (ceux qui ont les valeurs de S les plus grandes). Au bout de quelques cycles de reproduction, l'algorithme arrive à une solution acceptable mais on ne peut jamais être certain qu'il s'agit du minimum global. Notez également que l'algorithme génétique est un algorithme heuristique³ : il n'aboutit pas forcement au même résultat quand il est lancé deux fois de suite.

En réalité, comprendre dans les moindres détails le fonctionnement d'un algorithme génétique n'est pas vraiment nécessaire pour un biologiste. Nous utilisons une fonction Matlab nommée "ga" et c'est exactement comme pour le solveur numérique "ode45": ces fonctions sont des boites noires dont il n'est pas vraiment nécessaire de connaître totalement le fonctionnement sous jacent. Elles "font le job et elles le font bien".

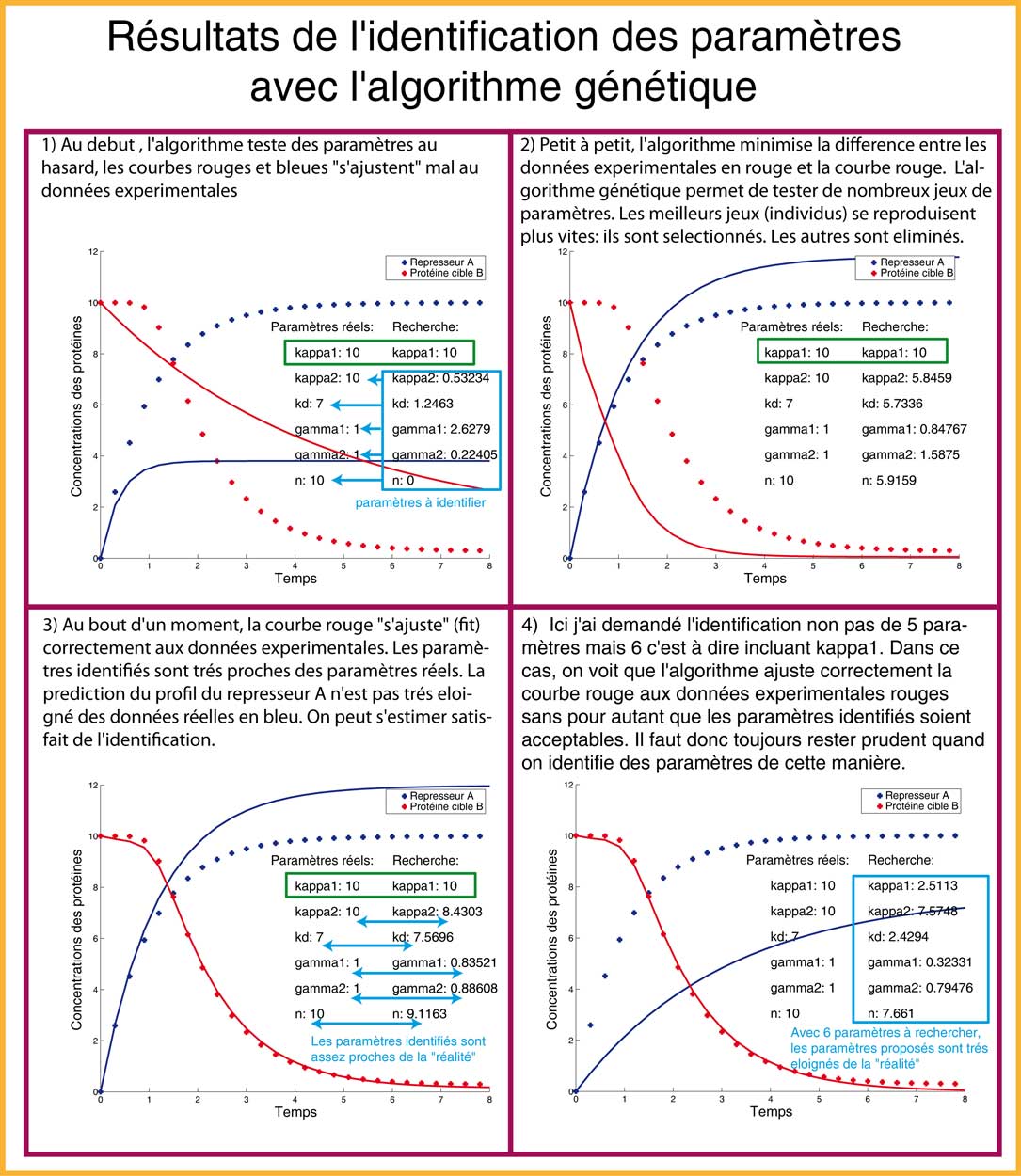
Figure 10. Résultats de l'identification des paramètres (les vidéos permettent de mieux visualiser le processus).

Dans le script Matlab, je confie le système des 2 équations différentielles à la fonction ode45 pour qu'elle l'intègre. Cette fonction ode45 est elle-même confiée à l'algorithme génétique (la fonction ga) qui s'occupe de faire varier puis de sélectionner les bons paramètres avec "sa population" cachée dans la boite noire. Puis quand l'algorithme a terminé, il ne nous reste plus qu'à comparer les paramètres réels (faussement expérimentaux) avec les paramètres estimés par le modèle.

Figure 11. Visualisation de la recherche des paramètres avec un algorithme génétique. Ici, les paramètres proposés sont cohérents. Voir le code Matlab ci-dessous qui gènère cette video.

Cliquer pour voir le code Matlab

                
% Identification de paramètres à l'aide d'un algorithme genetique.
% ce script necessite la toolbox "genetic algorithm"
function IdentificationParametre

%pour creer le film: decommenter le code film à plusieurs endroits dans le
%script
%crée un objet avi dans lequel on ajoute des frames pour la video
%code film
%mov = avifile('FilmGA','fps',5,'quality',100,'compression','none');

%% "Invention" des données experimentales
kappa1=10;%taux de synthese 
kappa2=10;%taux de synthese 
kd=7;%constante de dissociation
gamma1=1;%taux de degradation
gamma2=1;%taux de degradation
n=10;%paramètre de hill 

y0=[0, 10];%conditions initiales
Options = odeset('NonNegative',[1,2]);
Time=[0:0.3:10];
[t,dydt]=ode45(@equations,Time,y0, Options);%solveur numerique

% on crée une figure dans laquelle on met les données reels qui seront
% recherché par la suite par l'algorithme génétique
f=figure('Color', 'w');
axis([0 8 0 12]);
hold on
plot(t, dydt(:,1),'+b','LineWidth',3);% plot le represseur A
%Notez seul B est "donné" en input à l'algo génétique(données experimtales)
plot(t, dydt(:,2),'+r','LineWidth',3);% plot la concentration de B 
text(3.5,9,'Paramètres réels:')
text(4,8,['kappa1: ' num2str(kappa1)])
text(4,7,['kappa2: ' num2str(kappa2)])
text(4,6,['kd: ' num2str(kd)]) 
text(4,5,['gamma1: ' num2str(gamma1)])
text(4,4,['gamma2: ' num2str(gamma2)])
text(4,3,['n: ' num2str(n)]) 
xlabel('Temps','FontSize',16)
ylabel('Concentrations des protéines','FontSize',16)
title('Identification des paramètres avec un algorithme génétique',...
    'FontSize',14)
legend('Represseur A','Protéine cible B');
ExpData=dydt; %stoc les données experimentales

%% mise en place de l'optimisation 
ParamGene1=[0 0 0 0 0 0];% 
LB1=[0 0 0 0 0 0];
UB1=[20 20 20 20 20 20];

GAoptions1 = gaoptimset('Display','off','Generations',150);
it=0; % parametre pour le film (aucune importance)
ParamGeneOptim1 = ga(@optimregGA1,length(ParamGene1),...
    [],[],[],[],LB1,UB1,[],GAoptions1);

kappa1=ParamGeneOptim1(6);
kappa2=ParamGeneOptim1(2);
kd=ParamGeneOptim1(4);
gamma1=ParamGeneOptim1(3);
gamma2=ParamGeneOptim1(5);
n=ParamGeneOptim1(1);

%% plot des resultats finales
y0=[0, 10];
Options = odeset('NonNegative',[1,2]);
Time=[0:0.3:10];
[t,dydt]=ode45(@equations,Time,y0, Options);

plot(t, dydt(:,1),'-b','LineWidth',2)
plot(t, dydt(:,2),'-r','LineWidth',2)

text(6,9,'Recherche:')
text(6,8,['kappa1: ' num2str(kappa1)])
text(6,7,['kappa2: ' num2str(kappa2)])
text(6,6,['kd: ' num2str(kd)]) 
text(6,5,['gamma1: ' num2str(gamma1)])
text(6,4,['gamma2: ' num2str(gamma2)])
text(6,3,['n: ' num2str(n)]) 

%% fonction  utiliser par le GA
    function dydt = equations2(t,y,par)
        
        kappa1=par(6);
        kappa2=par(2);        
        kd=par(4);        
        gamma1=par(3);
        gamma2=par(5);        
        n=par(1);
        
        dydt=zeros(2,1);
        dydt(1) = kappa1- gamma1*y(1);
        dydt(2) = kappa2*(kd.^n/(kd.^n+y(1).^n))- gamma2*y(2);
        
    end
%% fonction utiliser pour générer les données experimentales
    function dydt = equations(t,y)
        
        dydt=zeros(2,1);
        dydt(1) = kappa1- gamma1*y(1);
        dydt(2) = kappa2*(kd.^n/(kd.^n+y(1).^n))- gamma2*y(2);
    end

%% fonction de la minimisation et de l'affichage
    function Optim=optimregGA1(PG)
        
        y0=[0, 10];
        Options = odeset('NonNegative',[1,2]);
        Time=[0:0.3:10];       
        [t,dydt]=ode45(@(t,y) equations2(t,y,PG),Time,y0,Options);
        
        p1=plot(t,dydt(:,1),'-b','LineWidth',2);
        p2=plot(t,dydt(:,2),'-r','LineWidth',2);
        
        t0=text(6,9,'Recherche:');
        t1=text(6,8,['kappa1: ' num2str(kappa1)]);
        t2=text(6,7,['kappa2: ' num2str(kappa2)]);
        t3=text(6,6,['kd: ' num2str(kd)]) ;
        t4=text(6,5,['gamma1: ' num2str(gamma1)]);
        t5=text(6,4,['gamma2: ' num2str(gamma2)]);
        t6=text(6,3,['n: ' num2str(n)]) ;
        
        it=it+1;
%code film        
%         if rem(it,15)==0
%         F=getframe(f);
%         mov = addframe(mov,F);
%         end
        
        pause(0.001);
        
        delete(p1);
        delete(p2);
        delete(t0);
        delete(t1);
        delete(t2);
        delete(t3);
        delete(t4);
        delete(t5);
        delete(t6);       

        if length(dydt(:,2))==length(ExpData(:,2))
            CLS = dydt(:,2)'-ExpData(:,2)';
            Optim = sum(CLS.^2); % somme des moindre carrés
        else
            Optim=inf;
        end
    end
%code film
%mov = close(mov);
end

Dans l'identification de paramètres visualisable sur la figure 11 (premier film) (ou figure 10 ; point numéro 3), on recherche 5 paramètres sur les 6 possibles (j'ai indiqué à l'algorithme la valeur de κ₁). Chacun peut observer que le fit des données expérimentales, les paramètres proposés ainsi que la prédiction d'évolution de [A] en fonction du temps sont loin d'être farfelus. Notre algorithme a prédit des valeurs très proches de la réalité pour les 5 paramètres. Vous avez donc ici une preuve en image que la modélisation peut incontestablement identifier/prédire des paramètres biologiques d'intérêt à partir de données expérimentales très limitées.

Figure 12. Le fit de l'éléphant: le risque "d'overfitting". Quand le nombre de paramètres devient trop grand, on peut "fitter" n'importe quoi sans pour autant que les paramètres proposés soient cohérents. Voir le code Matlab ci-dessous qui gènère cette video.

Cliquer pour voir le code Matlab

                
% algorithme qui montre que l'identification des paramètres peut echouer
%si le nombre de paramètres recherchés est trop grand.
function FitElephant
%pour creer le film: decommenter le code film à plusieurs endroits dans le
%script
%code film
%mov = avifile('FilmElephant','fps',5,'quality',100,'compression','none');

%% "Invention" des données experimentales
kappa1=10;
kappa2=10;
kd=7;
gamma1=1;
gamma2=1;
n=10;

y0=[0, 10];
Options = odeset('NonNegative',[1,2]);
Time=[0:0.3:10];
[t,dydt]=ode45(@equations,Time,y0, Options);

f=figure('Color', 'w');
axis([0 8 0 12]);
hold on

plot(t, dydt(:,1),'+b','LineWidth',3)
plot(t, dydt(:,2),'+r','LineWidth',3)

text(3.5,9,'Paramètres réels:')
text(4,8,['kappa1: ' num2str(kappa1)])
text(4,7,['kappa2: ' num2str(kappa2)])
text(4,6,['kd: ' num2str(kd)]) 
text(4,5,['gamma1: ' num2str(gamma1)])
text(4,4,['gamma2: ' num2str(gamma2)])
text(4,3,['n: ' num2str(n)]) 

xlabel('Temps','FontSize',16)
ylabel('Concentrations des protéines','FontSize',16)
title('Identification des paramètres avec un algorithme génétique','FontSize',14)
legend('Represseur A','Protéine cible B');

ExpData=dydt; %stoc les données experimentales

%% mise en place de l'optimisation 
ParamGene1=[0 0 0 0 0 0];
LB1=[0 0 0 0 0 0];
UB1=[20 20 20 20 20 20];

GAoptions1 = gaoptimset('Display','off','Generations',150);
it=0; % parametre pour le film (aucune importance)
ParamGeneOptim1 = ga(@optimregGA1,length(ParamGene1),[],[],[],[],LB1,UB1,[],GAoptions1);

kappa1=ParamGeneOptim1(6);
kappa2=ParamGeneOptim1(2);
kd=ParamGeneOptim1(4);
gamma1=ParamGeneOptim1(3);
gamma2=ParamGeneOptim1(5);
n=ParamGeneOptim1(1);

%% plot des resultats finales
y0=[0, 10];
Options = odeset('NonNegative',[1,2]);
Time=[0:0.3:10];
[t,dydt]=ode45(@equations,Time,y0, Options);

plot(t, dydt(:,1),'-b','LineWidth',2)
plot(t, dydt(:,2),'-r','LineWidth',2)

text(6,9,'Recherche:')
text(6,8,['kappa1: ' num2str(kappa1)])
text(6,7,['kappa2: ' num2str(kappa2)])
text(6,6,['kd: ' num2str(kd)]) 
text(6,5,['gamma1: ' num2str(gamma1)])
text(6,4,['gamma2: ' num2str(gamma2)])
text(6,3,['n: ' num2str(n)]) 

%% fonction  utiliser par le GA
    function dydt = equations2(t,y,par)
        
        kappa1=par(6);
        kappa2=par(2);        
        kd=par(4);        
        gamma1=par(3);
        gamma2=par(5);        
        n=par(1);
        
        dydt=zeros(2,1);
        dydt(1) = kappa1- gamma1*y(1);
        dydt(2) = kappa2*(kd.^n/(kd.^n+y(1).^n))- gamma2*y(2);
        
    end
%% fonction utiliser pour générer les données experimentales
    function dydt = equations(t,y)
        
        dydt=zeros(2,1);
        dydt(1) = kappa1- gamma1*y(1);
        dydt(2) = kappa2*(kd.^n/(kd.^n+y(1).^n))- gamma2*y(2);
    end

%% fonction de la minimisation et de l'affichage
    function Optim=optimregGA1(PG)
        
        y0=[0, 10];
        Options = odeset('NonNegative',[1,2]);
        Time=[0:0.3:10];       
        [t,dydt]=ode45(@(t,y) equations2(t,y,PG),Time,y0,Options);
        
        p1=plot(t,dydt(:,1),'-b','LineWidth',2);
        p2=plot(t,dydt(:,2),'-r','LineWidth',2);
        
        t0=text(6,9,'Recherche:');
        t1=text(6,8,['kappa1: ' num2str(kappa1)]);
        t2=text(6,7,['kappa2: ' num2str(kappa2)]);
        t3=text(6,6,['kd: ' num2str(kd)]) ;
        t4=text(6,5,['gamma1: ' num2str(gamma1)]);
        t5=text(6,4,['gamma2: ' num2str(gamma2)]);
        t6=text(6,3,['n: ' num2str(n)]) ;
        
        it=it+1;
%code film        
%         if rem(it,15)==0
%         F=getframe(f);
%         mov = addframe(mov,F);
%         end
        
        pause(0.001);
        
        delete(p1);
        delete(p2);
        delete(t0);
        delete(t1);
        delete(t2);
        delete(t3);
        delete(t4);
        delete(t5);
        delete(t6);       

        if length(dydt(:,2))==length(ExpData(:,2))
            CLS = dydt(:,2)'-ExpData(:,2)';
            Optim = sum(CLS.^2); % somme des moindre carrés
        else
            Optim=inf;
        end
    end
%code film
%mov = close(mov);
end

Mais je vais maintenant tempérer mes propos avec un contre-exemple. Il est également tout à fait possible que le modèle propose un ajustement (un fit) aux données expérimentales de bonne qualité alors même que les paramètres proposés sont complètement farfelus (figure 10 ; point numéro 4). On utilise souvent la métaphore "du fit de l'éléphant" qui signifie qu'à partir d'un certains nombres de paramètres, on peut ajuster (fitter) n'importe quoi (par exemple un éléphant) sans pour autant que les paramètres proposés correspondent à ce que l'on recherche. Regardez la figure 12 (deuxième film), où l'on recherche non plus 5 mais tous les paramètres (6). A la fin, l'ajustement du modèle à la courbe rouge n'est pas si mauvais mais les paramètres identifiés sont très éloignés de la "réalité". Il faut donc garder un oeil critique sur des paramètres identifiés avec un modèle. Vérifications et recoupements sont nécessaires.

Bibliographie

Danchin, A. (2009). "Information of the chassis and information of the program in synthetic cells." Syst Synth Biol 3(1-4): 125-34.
de Jong, H., J. Geiselmann, et al. (2003). "Genetic Network Analyzer: qualitative simulation of genetic regulatory networks." Bioinformatics 19(3): 336-44.
Elf, J., G. W. Li, et al. (2007). "Probing transcription factor dynamics at the single-molecule level in a living cell." Science 316(5828): 1191-4.
Elowitz, M. B., M. G. Surette, et al. (1999). "Protein mobility in the cytoplasm of Escherichia coli." J Bacteriol 181(1): 197-203.
Glass, L. and S. A. Kauffman (1973). "The logical analysis of continuous, non-linear biochemical control networks." J Theor Biol 39(1): 103-29.
Holland, J. (1975). "Adaptation in Natural and Artificial Systems." University of Michigan Press
Li, G. W. and J. Elf (2009). "Single molecule approaches to transcription factor kinetics in living cells." FEBS Lett 583(24): 3979-83.
Llopis, P. M., A. F. Jackson, et al. "Spatial organization of the flow of genetic information in bacteria." Nature.
Poon, J., M. Bailey, et al. (1997). "Effects of molecular crowding on the interaction between DNA and the Escherichia coli regulatory protein TyrR." Biophys J 73(6): 3257-64.
Riggs, A. D., S. Bourgeois, et al. (1970). "The lac repressor-operator interaction. 3. Kinetic studies." J Mol Biol 53(3): 401-17.
Ropers, D., H. de Jong, et al. (2006). "Qualitative simulation of the carbon starvation response in Escherichia coli." Biosystems 84(2): 124-52.
Slutsky, M. and L. A. Mirny (2004). "Kinetics of protein-DNA interaction: facilitated target location in sequence-dependent potential." Biophys J 87(6): 4021-35.
von Hippel, P. H. and O. G. Berg (1989). "Facilitated target location in biological systems." J Biol Chem 264(2): 675-8.
Zhou, H. X., G. Rivas, et al. (2008). "Macromolecular crowding and confinement: biochemical, biophysical, and potential physiological consequences." Annu Rev Biophys 37: 375-97.

Notes de bas de page

La formule utilisée est: c_n^k=n!/(k!(n-k)!) où n est le nombre de gènes et k le nombre de gènes deletés.
Antoine Coulon, Le hasard au coeur de la cellule, Syllepse chapitre 3 p. 75.
Heuristique est un terme qui signifie l'art d'inventer, de faire des découvertes