Les systèmes dynamiques en biologie

Préambule

Dans ce chapitre, qui est la suite directe du chapitre précédent, nous allons étudier la dynamique de fonctionnement de petits réseaux simples.

Un réseau à deux gènes: l'interrupteur (toggle switch en anglais)

Commençons par étudier le toggle switch: un petit réseau comprenant deux gènes qui se répriment mutuellement par l'intermédiaire des deux protéines correspondantes. L'analyse théorique de ce motif a été effectuée il y a une dizaines d'années (Cherry and Adler 2000). L'implémentation biologique a été effectuée quasiment au même moment (Gardner et al. 2000).

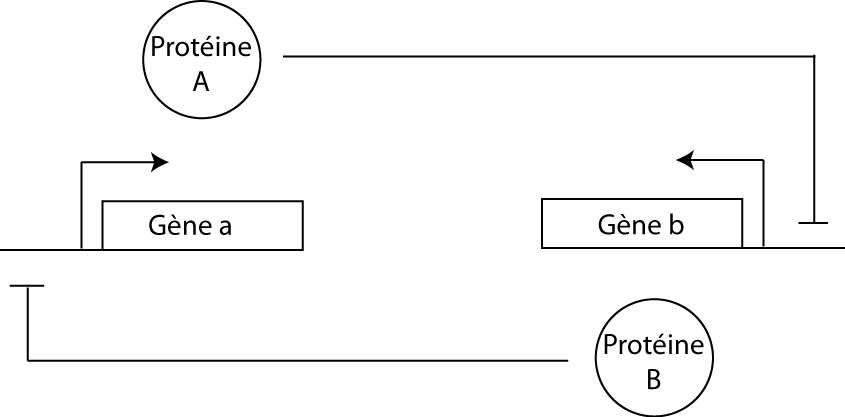
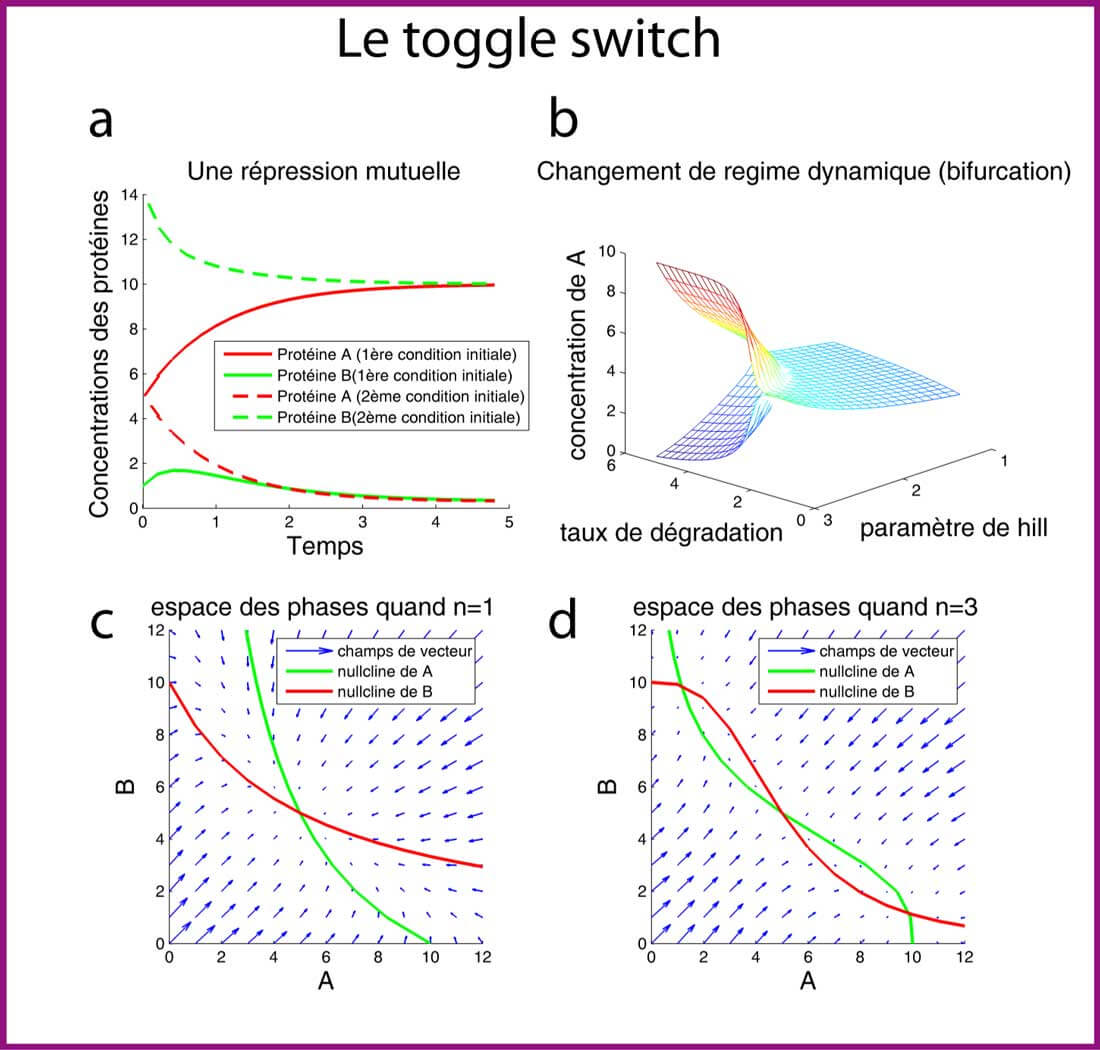
Suivant les conditions initiales, les concentrations des protéines A et B peuvent atteindre deux états d'équilibre différents (et opposés): on dit que le système est bistable. En effet, si A et B sont respectivement en forte et faible concentration au départ de la cinétique, le système atteint un état d'équilibre avec beaucoup de A et peu de B car la présence de A réprime l'expression de B. A l'inverse, l'état d'équilibre opposé sera atteint si c'est B qui est majoritaire au départ empêchant ainsi l'expression de A (figure 3a). Ce motif a été appelé "interrupteur" car en perturbant/changeant suffisamment la concentration d'une des protéines (en réalité son affinité pour le promoteur dans l'implémentation biologique), on peut faire "switcher" le système dans l'autre état stable.

Les cinétiques (concentrations en fonction du temps) n'offrent pas toujours la meilleure perspective pour comprendre le comportement d'un système dynamique. Il faut parfois recourir à l'espace des phases c'est-à-dire à un espace abstrait dont les coordonnées sont les variables dynamiques du système. Dans cette espace des phases, on peut tracer les deux "nullclines" c'est-à-dire les valeurs de B en fonction de A tel que d[B]/dt=0. On obtient facilement l'équation suivante:

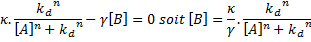
Et réciproquement les valeurs de A en fonction de B tel que d[A]/dt=0 soit

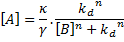
A l'intersection de ces "nullclines", ni la concentration de A ni la concentration de B ne changent. Par conséquent, en ces points fixes, le système est à l'état stable (figure 3d).

Il peut être aussi utile de tracer un champ de vecteur nous indiquant le taux de changement des variables du système à différents points dans le diagramme de phase (correspondant par exemple à la condition initiale). En prenant le coté gauche de l'équation différentielle (le taux de changement en fonction du temps) de chacune des deux équations du modèle, on construit un vecteur dont la longueur indique le taux auquel le système change d'état et la direction indique où le système est dirigé dans l'espace des phases. Par exemple, si d[B]/dt=4 et d[A]/dt=-2 avec B tracé sur l'axe horizontal et A sur l'axe vertical alors le vecteur pointe en bas à droite comme montré ci-dessous.

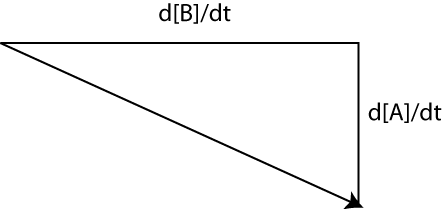
Dans la figure 3d (où le paramètre de coopérativité n est fixé à 3), les "nullclines " se croisent en trois points: il y a trois états stables: deux états stables "stables" où la concentration de A est forte et celle de B est faible (et réciproquement) et un état stable " instable" qui correspond à des concentrations de A et B identiques. On observe que beaucoup de vecteurs tendent déjà vers cet état instable puis bifurquent vers l'un ou l'autre des deux autres états stables.

Dans la figure 3c , le paramètre de coopérativité n est fixé à 1. Dans ce cas, on observe que les "nullclines" se croisent en un point unique: le seul point d'équilibre du système (figure 3c). Cela a une importante conséquence: cela signifie que le phénotype qu'exhibe un système dynamique (par exemple la bistabilité) dépend fortement de la valeur des paramètres. Ainsi, dans notre exemple, pour une même topologie du réseau (répression mutuelle), le système peut exhiber une dynamique bistable ou monostable en fonction de la valeur des paramètres. Ainsi, pour étudier le comportement d'un système dynamique, il faut aussi travailler dans l'espace des paramètres. Lorsque qu'un certain seuil dans la valeur numérique d'un paramètre est dépassé, le système passe soudainement d'un régime dynamique monostable à un régime dynamique bistable. Cette transition soudaine s'appelle une bifurcation. Dans la figure 3b, on trace le ou les états stables de la concentration de A en fonction du taux de dégradation et du paramètre de Hill. On voit bien s'opérer la bifurcation entre les deux régimes dynamiques (monostable versus bistable).

                
function ToggleSwitch
clear all
figure('Color', 'w')
hold on
for i=1:4 % genere 4 petit plots et leur attribut un "handle"
    Handle(i)=subplot(2,2,i);
    hold(Handle(i));  
end
Vector=[];
VectorPool1=[];
VectorPool2=[];
% système d'équation differentielle avec la repression mutuelle
function dydt = equations(t,y)
    dydt=zeros(2,1);    
    dydt(1) = kappa*(kd.^n/(kd.^n+y(2).^n))- gamma*y(1); % A
    dydt(2) = kappa*(kd.^n/(kd.^n+y(1).^n))- gamma*y(2); % B
end
n=5;% paramètre de hill
kappa=10;% taux de synthese
kd=5;% consante de dissociation
gamma=1;% taux de dégradation

y1=5;% conditions initiales de A

it=0; % pour les iterations

for n=5:-0.2:1 % boucle qui fait varier n 
     it=it+1;
for gamma=1:0.1:3 % boucle qui fait varier gamma

 for y2=[1 14] % conditions initiales de B
yo=[y1 y2];
    Options = odeset('NonNegative',[1,2]);
Time=[0:0.2:20];
[t,dydt]=ode45(@equations,Time,yo, Options);

%% plot numero 1 (fait varier la condition initiale  de Y et montre que
%% le systeme bascule dans deux états stables differents

if n==5 && gamma==1
    if y2==14 % quand conditions initiales de B plus grandes que celle de A
plot(Handle(1),t(1:25), dydt(1:25,1),'--r','LineWidth',2)
plot(Handle(1),t(1:25), dydt(1:25,2),'--g','LineWidth',2)
    else  % quand conditions initiales de A plus grandes que celle de B
plot(Handle(1),t(1:25), dydt(1:25,1),'r','LineWidth',2)
plot(Handle(1),t(1:25), dydt(1:25,2),'g','LineWidth',2)
    end
    
xlabel(Handle(1),'Temps','FontSize',16)
ylabel(Handle(1),'Concentrations des protéines','FontSize',16)
title(Handle(1),'Une répression mutuelle','FontSize',16)
legend(Handle(1),'Protéine A (1ère condition initiale)'...
,'Protéine B(1ère condition initiale)'...
,'Protéine A (2ème condition initiale)'...
,'Protéine B(2ème condition initiale)');
end

%% plot numero 2 (une fronce/bifurcation/cusp en anglais)
%on fait varier le parametre de hill n et le taux de degradation gamma et
%on montre que la dynamique du systeme passe de 1 à 2 états stables.
Vector=[Vector dydt(end,1)];

 end
Vector1=max(Vector);
Vector2=min(Vector);
Vector=[];
VectorPool1=[VectorPool1 Vector1];
VectorPool2=[VectorPool2 Vector2];
end
VectorFin1(it,:)=VectorPool1;
VectorFin2(it,:)=VectorPool2;
VectorPool1=[];
VectorPool2=[];
end
mesh(Handle(2),5:-0.2:1,3:-0.1:1,VectorFin1')
mesh(Handle(2),5:-0.2:1,3:-0.1:1,VectorFin2')
view(Handle(2),-143,17);
zlabel(Handle(2),'concentration de A','FontSize',16)
ylabel(Handle(2),'paramètre de hill','FontSize',16)
xlabel(Handle(2),'taux de dégradation','FontSize',16)
title(Handle(2),'Changement de regime dynamique (bifurcation)','FontSize',16)
%legend(Handle(1),'Protéine A','Protéine B');

%% plot numero 3 et 4: espaces des phases,  nullclines et  champs de
%% vecteurs
for n=[1 3]% compare l'espace des phases pour deux valeurs de n
gamma=1;% refixe gamma;   
[a,b]=meshgrid(0:1:12,0:1:12);
dadt = kappa*(kd.^n./(kd.^n+b.^n))- gamma.*a;
dbdt = kappa*(kd.^n./(kd.^n+a.^n))- gamma.*b;
if n==1
quiver(Handle(3),a,b,dadt,dbdt,'LineWidth',1); % trace le champs de vecteur pour n=1
end

if n==3
quiver(Handle(4),a,b,dadt,dbdt,'LineWidth',1);% trace le champs de vecteur pour n=3
end

b=0:1:12;
a=kappa*(kd.^n./(kd.^n+b.^n))./gamma;% nullcline de a (dans ce cas 
%précis celui de b est identique); pour me faciliter la tache, je change
%juste l'ordre des absisses et ordonnées dans le plot

if n==1
plot(Handle(3),a,b,'-g','LineWidth',2)
plot(Handle(3),b,a,'-r','LineWidth',2)
xlabel(Handle(3),'A','FontSize',16)
ylabel(Handle(3),'B','FontSize',16)
title(Handle(3),'espace des phases quand n=1','FontSize',16)
legend(Handle(3),'champs de vecteur','nullcline de A','nullcline de B')
end
if n==3
plot(Handle(4),a,b,'-g','LineWidth',2)
plot(Handle(4),b,a,'-r','LineWidth',2)
xlabel(Handle(4),'A','FontSize',16)
ylabel(Handle(4),'B','FontSize',16)
title(Handle(4),'espace des phases quand n=3','FontSize',16)
legend(Handle(4),'champs de vecteur','nullcline de A','nullcline de B')
end
axis(Handle(4),'square')
axis(Handle(4),'tight')
axis(Handle(3),'square')
axis(Handle(3),'tight')
end
end
                
            

Hystérésis induite par une boucle de rétroaction positive

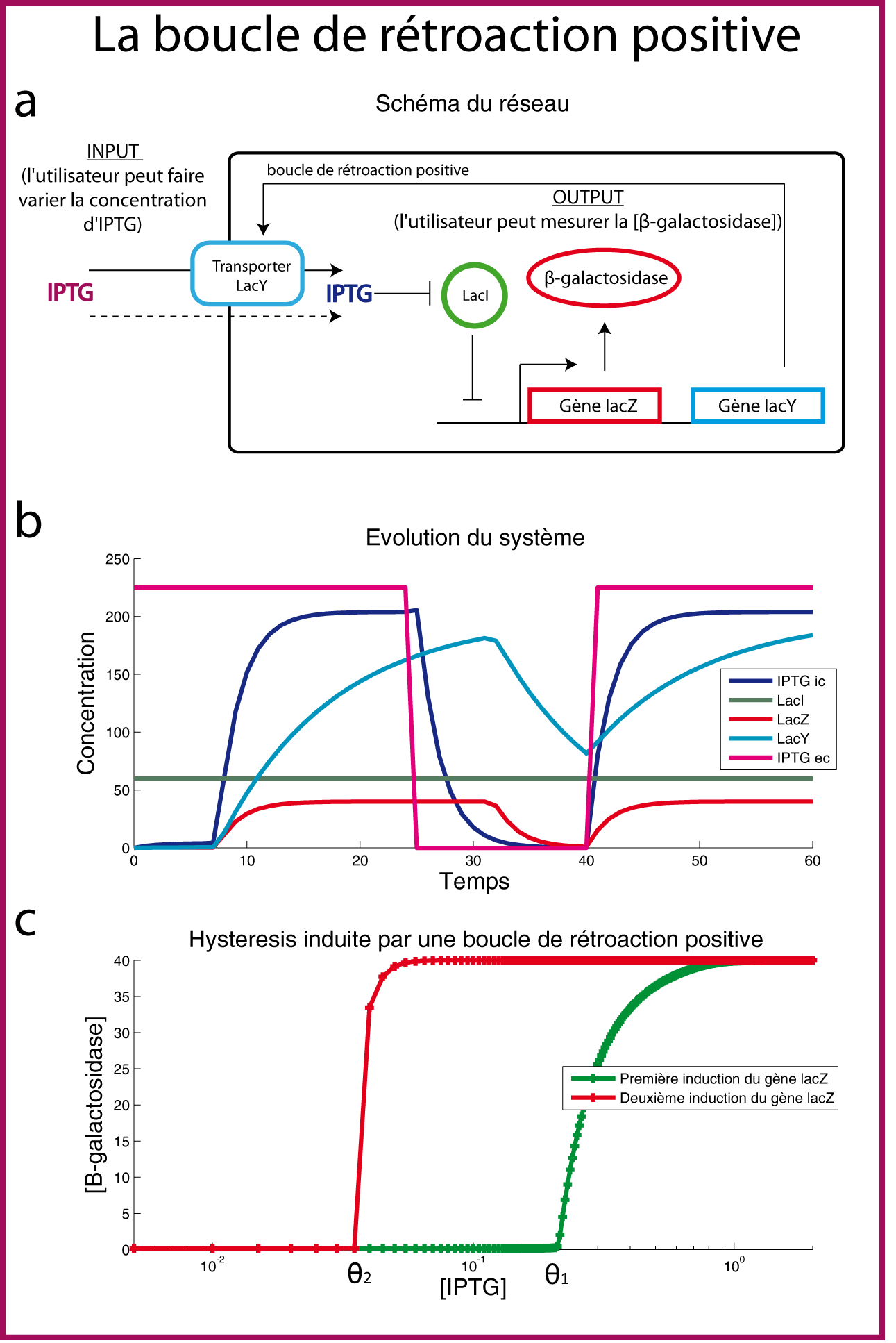
Etudions maintenant un autre type de réseau bistable: la boucle de rétroaction positive. L'exemple très classique de l'induction bistable de l'operon lactose est connu depuis plus de cinquante ans (Novick and Weiner 1957; Cohn and Horibata 1959). C'est un réseau qui est maintenant bien caractérisé mais qui reste encore très étudié aujourd'hui (Robert et al.; Ozbudak et al. 2004; Chang et al. 2009). Le réseau dont nous allons modéliser le fonctionnement est une version simplifiée (figure 4a) à laquelle j'ai retiré la répression catabolique (le complexe Crp--cAMP). Dans ce réseau, l'expérimentateur contrôle la concentration de l'IPTG dans le milieu (l'input). Cet IPTG pénètre la cellule de manière "transporteur indépendante " et se fixe au répresseur LacI. Ce dernier change alors de conformation ce qui diminue fortement son affinité pour le promoteur de l'operon lac. L'absence du répresseur sur le promoteur a pour conséquence la transcription des gènes lacZ et lacY. Le gène lacZ code pour une enzyme (la β-galactosidase) dont il est facile de mesurer la concentration (voir le chapitre sur les interactions): c'est l'output. Le gène lacY code pour le transporteur LacY. Une fois dans la membrane, ce dernier augmente fortement le transport de l'IPTG (cette fois de manière transporteur dépendante). Comme l'import d'IPTG augmente, il y a plus de transcription de lacY ce qui augmente à nouveau l'import d'IPTG et ainsi de suite. C'est le principe d'une boucle de retro-action positive.

La figure 4b nous montre l'évolution prédite par le modèle numérique des différentes concentrations des composés en fonction du temps. Au début, jusqu'au temps 7, comme l'import de l'IPTG extracellulaire est limité, la concentration de la β-galactosidase et du transporteur augmente très lentement. Puis, lorsque la concentration du transporteur dépasse un certain seuil (temps 7), la boucle de rétroaction se met en place et les concentrations d'IPTG, de β-galactosidase et du transporteur explosent puis atteignent leur état d'équilibre (temps 24). Au temps 25, on imagine que l'expérimentateur enlève l'IPTG du milieu. Concrètement, il centrifuge les cellules, remplace le surnageant par du milieu sans IPTG puis resuspend les cellules dans le nouveau milieu. En absence d'IPTG, le répresseur réprime à nouveau l'operon lac et la transcription s'arrête. La β-galactosidase et le transporteur LacY se dégradent selon leur taux de dégradation respectif. Au temps 40, il n'y a plus de β-galactosidase mais il y a encore le transporteur ce qui fait que, contrairement à ce qui se passe à t=0, le nouvel ajout d'IPTG active immédiatement la transcription de l'operon lac.

                
function Hysteresis
%petit fonction qui illustre  l'hysteresis observé avec une boucle de
%retroaction positive

%% gestion de la figure
clear all
figure('Color', 'w')
for i=1:2
    Handle(i)=subplot(2,1,i);
    hold(Handle(i));
end
Condition1=[];
Condition2=[];
%% système d'equations differentielle
% l'IPTG est ajouté par l'experimentateur à t=0 puis enlevé à t=25
%(centrifugation  des bactéries et resuspension dans du milieu frais).
%Puis on ajoute à nouveau de l'IPTG à t=50.
    function dydt = equations(t,y)
dydt=zeros(4,1);
Iptg_ext=IPTG*(t<25||t>40);% IPTG extracellulaire
dydt(1) = (kappa1*Iptg_ext + kappa2*Iptg_ext*(y(4).^n...
    /(kd3.^n+y(4).^n))- gamma1*y(1));% IPTG intracellulaire
dydt(2) = kappa3-gamma2*y(2);% LacI (non regulé et donc considéré constant)
dydt(3) = kappa4*(kd.^n/(kd.^n+ (y(2)-(y(2)...
    *y(1).^n/(kd2.^n + y(1).^n)))))- gamma3*y(3);%LacZ
dydt(4) = kappa4*(kd.^n/(kd.^n+(y(2)-(y(2)*y(1).^n...
    /(kd2.^n + y(1).^n)))))- gamma4*y(4);% LacY
    end
%% paramètres (totalement arbitraire)
n=10;% paramètre de hill
kappa1=2;% taux d'import de l'IPTG de manière permease independante
kappa2=100;% taux d'import de l'IPTG via LacY
kappa3=30;% taux de synthèse de LacI
kappa4=20;% taux de synthèse de LacZ et LacY

kd=0.87;% constante de dissociation de LacI sur le promoteur de l'operon 
%lac
kd2=4;% constante de dissociation de l'IPTG sur LacI
kd3=0.87;% constante de dissociation de l'IPTG sur LacY
gamma1=0.5;% taux d'export de l'IPTG
gamma2=0.5;%taux de degradation de LacI
gamma3=0.5;%taux de degradation de LacZ
gamma4=0.1;%taux de degradation de LacY

%% le code ci dessous montre l'evolution des concentrations en fonction du
%% temps et le graphe d'hysteresis.  
%% la gestion des deux graphes en même temps complique un peu le code mais
%% le raccourci

%i=1; la cellule n'a jamais vu l'IPTG ni induit LacY. 
%i=2; la cellule "se rappelle" de l'IPTG car elle a encore des LacY
for i=1:2    
% on fait varier la concentration d'IPTG extracellulaire
    for IPTG=[0.005:0.005:2]
        yo=[0 60 0 0];% conditions initiales          
% lors du deuxieme ajout d'IPTG, les cellules ont la concentration de LacY
%obtenu pour i=1 au temps 40        
        if i==2
            yo(4)=y(40,4);
        end
% integration du systeme d'equations differentielles        
        Options = odeset('NonNegative',[1 2 3 4]);
        Time=[0:1:60];
        [t,y]=ode45(@equations,Time,yo,Options);
% gestion du graphe des concentrations en fonction du temps       
        if IPTG==1 && i==1
            plot(Handle(1),t,y,'LineWidth',3)
            xlabel(Handle(1),'Temps','FontSize',16)
            ylabel(Handle(1),'Concentration','FontSize',16)
            title(Handle(1),'Evolution du système','FontSize',16)
            plot(Handle(1),t,225*IPTG*(t<25|t>40),'color','m',...
                'LineWidth',3)
            legend(Handle(1),'IPTG ic','LacI','LacZ','LacY','IPTG ec');
        end
        if  i==1
            Condition1=[Condition1 y(20,3)];
        end
        if  i==2
            Condition2=[Condition2 y(20,3)];
        end        
    end
end
% graphe de l'hysteresis
plot(Handle(2),0.005:0.005:2,Condition1,'-+g','LineWidth',3)
plot(Handle(2),0.005:0.005:2,Condition2,'-+r','LineWidth',3)
xlabel(Handle(2),'[IPTG]','FontSize',16)
ylabel(Handle(2),'[B-galactosidase]','FontSize',16)
title(Handle(2),['Hysteresis induit par une boucle'...
'de retro-action positive'],'FontSize',16);
legend(Handle(2),'Première induction du gène lacZ'...
    ,'Deuxième induction du gène lacZ');
set(Handle(2),'XScale','log')
axis(Handle(2),[0.005 2 0 40])
end
                
            

Et vous allez me dire, oui et alors ? Pourquoi cela est-il si intéressant ? Cela est intéressant car d'un point de vue "informatique", entre T=0 et T=25 on a "écrit" une information et au temps t=40, on a "lu" cette information. La cellule, ici, a joué le rôle de mémoire, elle a stocké un bit d'information. Encore une fois nous retrouvons l'analogie cellule--ordinateur. Rentrons maintenant en peu dans le détail en présentant le phénomène d'hystérésis. L'hystérésis c'est la propriété d'un système qui tend à demeurer dans un certain état quand la cause extérieure qui a produit le changement d'état a cessé. Pour bien illustrer ce phénomène, faisons une expérience de pensée (expérience simulée "in silico" dans la figure 4c). Imaginez que l'on place les cellules " naives ; bit=0" (c'est-à-dire celles à t=0 qui n'ont jamais connu l'IPTG) dans un milieu et que l'on augmente petit à petit l'IPTG. Lorsque qu'un certain seuil θ_1 est dépassé, la concentration d'IPTG devient suffisante pour activer la boucle de rétroaction et induire l'expression de la β-galactosidase (courbe verte): le bit passe de 0 à 1 et on a "écrit" une information. Faisons-la même expérience mais cette fois en prenant les cellules "initiées, bit=1" mais sans β-galactosidase (cellules à t=40). On augmente petit à petit l'IPTG mais cette fois le seuil θ_2, nécessaire pour induire l'expression de la β-galactosidase est beaucoup plus faible (courbe rouge) car les cellules avaient déjà le transporteur. Maintenant supposez que l'on soit en possession de cellules dont on ne sait pas si elles sont "naïves, bit=0" ou " initiées ; bit=1". Il suffit de placer les cellules à une concentration d'IPTG comprise entre θ_2 et θ_1. Si les cellules induisent la β-galactosidase, elles sont "initiées " et le bit était égal à 1. A l'inverse, si elles n'induisent pas la β-galactosidase, alors elles sont "naïves" et le bit était égal à 0. En se plaçant à une concentration d'IPTG intermédiaire entre θ_2 et θ_1, on a "lu" une information stockée en mémoire.

J'aimerai préciser ici que les phénomènes de bistabilité que nous avons étudiés dans ce chapitre sont toujours modélisés de manière déterministe comme si toutes les cellules se comportaient de la même manière. Sachez que la conséquence principale de ces phénomènes de bistabilité s'observe en comparant les cellules entre-elles. Pour un même génotype et dans le même milieu, les bactéries se partageront en deux groupes avec deux phénotypes bien distincts. Mais ne vous inquiétez pas, j'y reviendrai largement lorsque nous aborderons le bruit, les stratégies de pari et la modélisation stochastique. Et nous n'y sommes pas encore.

Un réseau à trois gènes: le repressilator

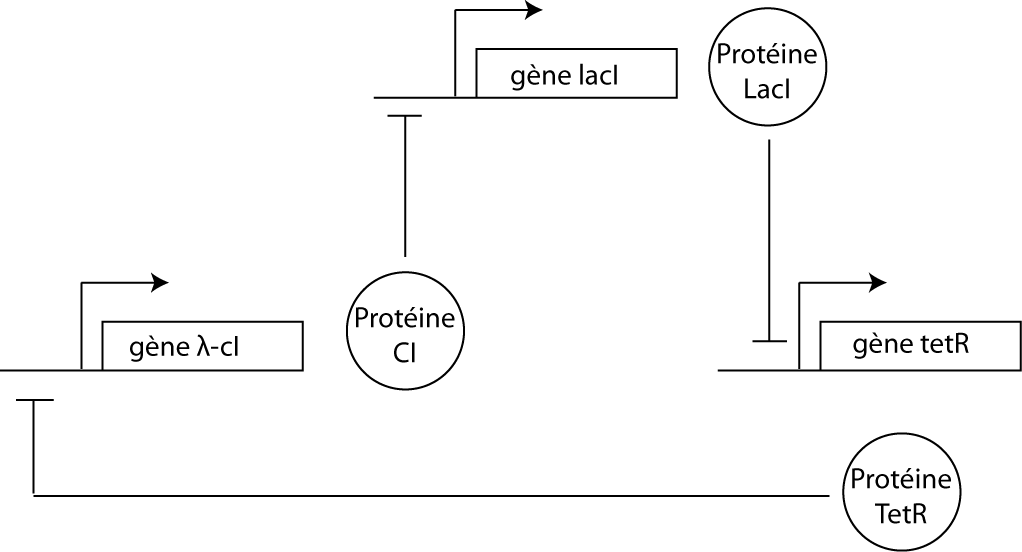
La topologie de certains réseaux permet aux concentrations des protéines impliquées de ne jamais atteindre un état stable, d'osciller en permanence au cours du temps. Le "repressilator" est un exemple de ce type de réseau. Il a été implémenté biologiquement (sur un plasmide) en l'an 2000 par Michael Elowitz (Elowitz and Leibler 2000). Il est composé de 3 gènes qui se répriment mutuellement ce qui permet l'apparition d'oscillations dans la concentration des trois protéines (figure 5). Plutôt que d'appeler les protéines A, B et C, J'ai préféré conserver le nom de protéines utilisées car elles sont très communes et tout biologiste synthétique y aura à faire un jour ou l'autre. Il s'agit des répresseurs LacI, TetR et CI.

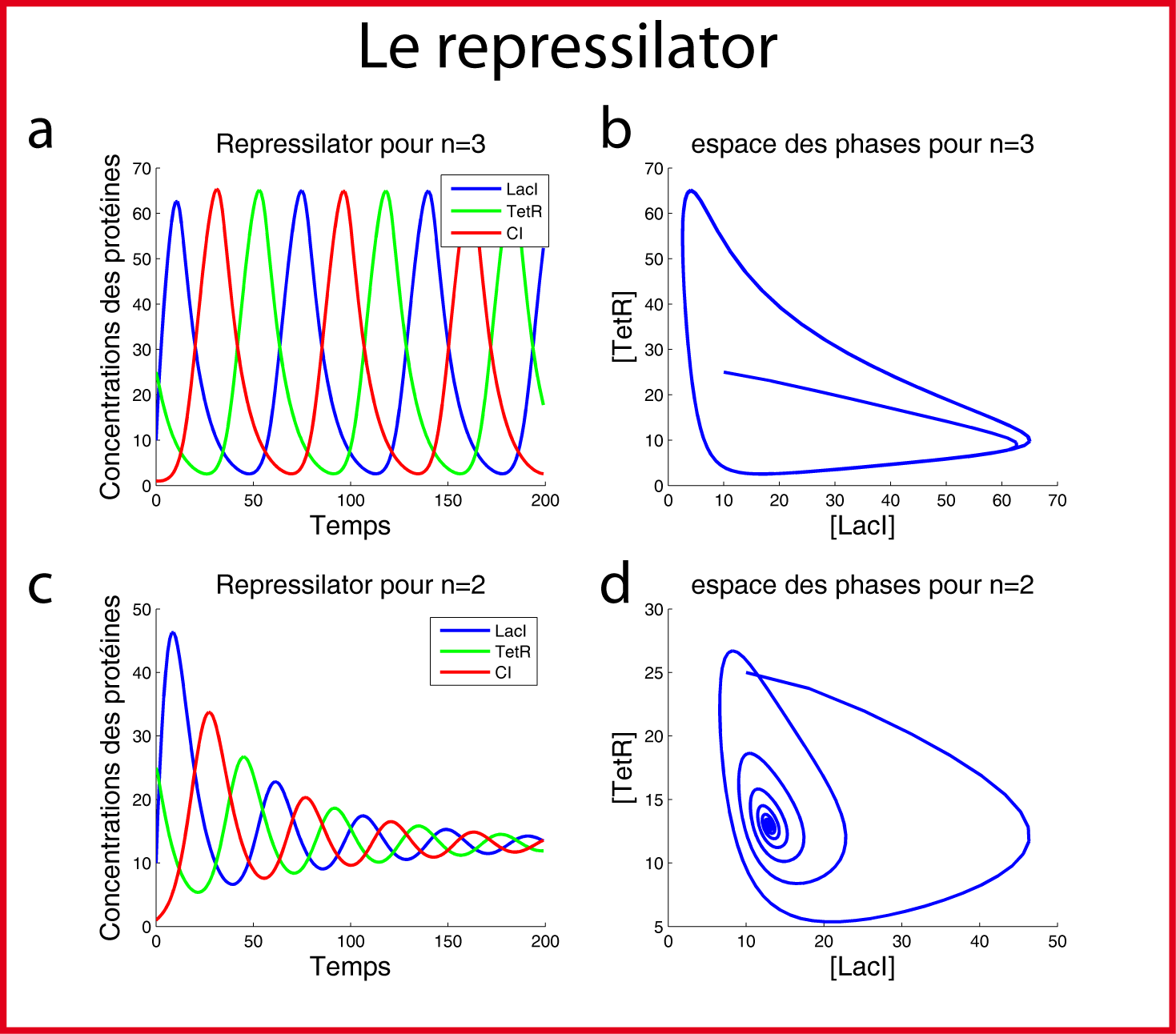
Au regard des résultats de simulation (figure 6a), on observe bien l'oscillation des 3 protéines en fonction du temps. De plus, on observe une nouvelle fois que la topologie seule n'est pas suffisante pour déterminer le comportement du système: la valeur numérique des paramètres compte. En effet, dans notre simulation, lorsque le paramètre de Hill est fixé à 3, les oscillations perdurent et le système n'atteint jamais un état stable. A l'inverse, lorsque ce paramètre est fixé à 2, les oscillations s'atténuent et le système finit par atteindre un état stationnaire (figure 6a vs 6c).

Comme je l'ai déjà dit plus haut, l'esprit a des difficultés à prédire de manière certaine la dynamique de fonctionnement de réseaux très simples. Et il me semble très peu probable que Michael Elowitz ait construit son plasmide "repressilator" sans préalablement avoir vérifié "in silico " que la topologie du réseau était bien en mesure de générer des oscillations. Le modèle peut, par exemple, aider à moduler la période ou l'amplitude des oscillations en indiquant a priori quel paramètre modifier. Par exemple, pour diminuer la période des oscillations, on peut diminuer le taux de dégradation des protéines. Pour cela, on clone un tag "ssra" en 3' de la séquence codante de l'ADN. Cela rajoute les acides aminés ANDENYALAA en 3' de la protéine. Cette séquence adresse les protéines vers le proteasome augmentant ainsi leurs taux de dégradation. Avant d'entreprendre des manipulations fastidieuses de biologie moléculaire, il est prudent et facile de vérifier qu'en diminuant le "gamma" dans le modèle, cela diminue bien la période des oscillations.

Petit parenthèse ici puisque l'on vient de voir comment changer gamma. Comment peut-on changer le taux de synthèse Kappa ou la constante de dissociation k_d "pour de vrai" ? Pour changer Kappa, on peut modifier par mutagenèse dirigée un ou plusieurs nucléotides de la "TATA box" (lieu où se fixe l'ARN polymérase) ou du "ribosome binding site (RBS)" (lieu où se fixe le ribosome) pour diminuer respectivement le nombre d'évènements de transcription ou de traduction. Même méthode pour modifier la constante de dissociation: on change par mutagenèse dirigée les nucléotides du site de fixation à l'ADN après avoir bien étudié le motif consensus pour diminuer ou augmenter l'affinité du facteur de transcription pour ce site.

La video 1 montre des bactéries contenant la "green fluorescent protein" (GFP) dont la concentration oscille au cours du temps. Ce n'est pas exactement le "repressilator " mais un système dynamique oscillant un peu plus récent et donc plus joli mais à peine plus complexe (Stricker et al., 2008). La vidéo est le fruit du travail de leurs auteurs. Je l'ai ajoutée ici avec leurs autorisations. Je souhaitais absolument l'inclure (et pas seulement mettre un lien hypertexte) car elle illustre ce qu'est la biologie synthétique et surtout ce qu'elle promet. Rendez vous compte, les oscillations de la GFP que vous regardez sur cette video ont été encodées sur un morceau d'ADN par un être humain. Les auteurs peuvent même contrôler la période des oscillations (entre 10 et 40 minutes). Je ne sais pas si vous serez d'accord avec moi mais je trouve que cela rend beaucoup moins futuriste l'idée de faire du calcul avec des cellules et donc avec de la matière "humide" (dite Wetware par opposition aux puces électroniques "sèches" dites Hardware).

Cependant, ce détour par la biologie synthétique ne doit pas vous laisser croire que ces oscillateurs ne sont que des bizarreries sans intérêt créées par et pour l'homme. En effet, des oscillateurs moléculaires existent dans la nature et pas seulement chez les eucaryotes. On en trouve chez certaines archaebactéries (Kondo et al. 1993) (Mihalcescu et al. 2004). Ils sont utiles pour l'adaptation du contenu cellulaire au rythme circadien c'est-à-dire à l'alternance du jour et de la nuit.

                
function Oscillation

figure('Color', 'w')
hold on
for i=1:4 % genere 4 petit plots et leur attribut un handle
    Handle(i)=subplot(2,2,i);
    hold(Handle(i));
end
% systèmes de 3 equations differentielles
    function dydt=equations(t,y)
        
        dydt=zeros(3,1);
        dydt(1) = kappa*(kd.^n/(kd.^n+y(3).^n))- gamma*y(1);% LacI
        dydt(2) = kappa*(kd.^n/(kd.^n+y(1).^n))- gamma*y(2);% tetR
        dydt(3) = kappa*(kd.^n/(kd.^n+y(2).^n))- gamma*y(3);%CI
        
    end
for n=2:3% boucle qui regarde la dynamique du système pour n=2 puis n=3
    kappa=10; %taux de synthèse
    gamma=0.1; %taux de dégradation
    kd=5;% constante de dissociation
    
    y0=[10, 25, 1];% conditions initiales arbitraires   
    Options = odeset('NonNegative',[1,2,3]);
    [t,y]=ode45(@equations,[0:1:400],y0, Options);% integration numerique

    if n==3
        plot(Handle(1),t(1:200), y(1:200,1),'-b','LineWidth',2)
        plot(Handle(1),t(1:200), y(1:200,2),'-g','LineWidth',2)
        plot(Handle(1),t(1:200), y(1:200,3),'-r','LineWidth',2)
        plot(Handle(2),y(:,1),y(:,2),'LineWidth',2)
    end
    if n==2
        plot(Handle(3),t(1:200), y(1:200,1),'-b','LineWidth',2)
        plot(Handle(3),t(1:200), y(1:200,2),'-g','LineWidth',2)
        plot(Handle(3),t(1:200), y(1:200,3),'-r','LineWidth',2)
        plot(Handle(4),y(:,1),y(:,2),'LineWidth',2)
    end    
end
xlabel(Handle(1),'Temps','FontSize',16)
ylabel(Handle(1),'Concentrations des protéines','FontSize',16)
title(Handle(1),'Repressilator pour n=3','FontSize',16)
legend(Handle(1),'LacI','TetR','CI');
xlabel(Handle(3),'Temps','FontSize',16)
ylabel(Handle(3),'Concentrations des protéines','FontSize',16)
title(Handle(3),'Repressilator pour n=2','FontSize',16)
legend(Handle(3),'LacI','TetR','CI');

xlabel(Handle(2),'[LacI]','FontSize',16)
ylabel(Handle(2),'[TetR]','FontSize',16)
title(Handle(2),'espace des phases pour n=3','FontSize',16)

xlabel(Handle(4),'[LacI]','FontSize',16)
ylabel(Handle(4),'[TetR]','FontSize',16)
title(Handle(4),'espace des phases pour n=2','FontSize',16)
end
                
            

Caractéristiques des réseaux réels

On doit aux mathématiciens Paul Ërdos et Alfred Rényi les premiers travaux sur les réseaux aléatoires. Ces derniers sont composés de noeuds et de liens. Lorsque les liens sont placés aléatoirement, la plupart des noeuds ont, en moyenne, le même nombre de liens: le système est "démocratique". La distribution qui représente le nombre de liaisons par noeud a une allure de cloche: c'est une distribution de Poisson (figure 7). Cela signifie qu'il n'y a quasiment pas de noeuds ayant soit très peu soit énormément de liens (Barabasi & Bonaneau, 2010).

Mais les réseaux des organismes vivants ne sont pas des réseaux aléatoires. Ils possèdent la propriété d'invariance d'échelle (retrouvée aussi avec d'autres types de réseaux comme Internet) (Jeong et al., 2000, 2001; Ravasz et al., 2002). Quelques supernoeuds (des "hubs") possèdent un très grand nombre de liaisons avec d'autres noeuds qui eux, au contraire, sont très peu connectés. Dans le réseau internet, "google" est un de ces supernoeuds connecté au site web de tricot de votre grand-mère ---site sans doute très intéressant mais probablement peu connecté---. Dans le réseau de régulation génique d'E. coli, c'est la protéine Crp qui est un "hub" connecté à des enzymes moins "populaires". Contrairement à la distribution de Poisson "démocratique" des réseaux aléatoires, la distribution des réseaux invariants d'échelle suit une loi de puissance. Le nombre de liens par noeud décroit exponentiellement. Ces réseaux présentent certains comportements prévisibles. Par exemple, contrairement aux réseaux aléatoires, ils sont très résistants aux défaillances accidentelles mais extrêmement vulnérables aux attaques ciblées sur les "hubs" (figure 7).

Cependant, l'hypothèse selon laquelle les réseaux de régulation génique suivent une loi de puissance est contestée (Lima-Mendez & van Helden, 2009). Voici quelques arguments des contradicteurs:

• La loi de puissance n'apporterait aucune information nouvelle en biologie et serait donc sans intérêt réel.
• Les "hubs" ne sont pas toujours essentiels: la preuve c'est que le mutant crp est viable alors qu'un très grand nombre d'enzymes (noeuds très peu connectés) sont indispensables à la survie de la bactérie.
• Les données qui sont censées prouver la loi de puissance sont sur-interprétées.

Je rajoute un argument personnel: les réseaux tels qu'ils sont décrits actuellement avec leurs "hubs" (figure 8a) pourraient représenter plus le pool des expériences réussies par les chercheurs que la réalité biologique. Les "hubs" seraient les exemples/cas d'écoles les plus simples, les zones où les certitudes sont les plus fortes. Un noeud où les chercheurs convergent car les expériences y seraient plus facilement reproductibles. Je m'explique: j'en suis arrivé à travailler sur le "hub" Crp par dérive. J'ai commencé sur des gènes moins connus et dont la régulation est moins comprise. L'absence de résultats, de compréhension et de reproductibilité m'a fait dériver vers d'autres directions, là où les expériences offraient une meilleure reproductibilité. Petit à petit, de gènes en gènes, j'en suis arrivé à Crp. Si les chercheurs qui publient sur Crp ont subi une dérive similaire à la mienne, alors la quantité énorme d'informations accessible sur Crp est plus liée à la facilité/reproductibilité des expériences qu'à une réalité biologique selon laquelle Crp est un "hub ".

Malgré mon argument ci-dessus, considérons tout de même la figure 8a comme une représentation globalement fidèle du réseau transcriptionnel réel d'E. coli. Nous avons vu que ce réseau n'est pas aléatoire du point de vue de la distribution des liens par noeud. Mais il n'est pas aléatoire également du point de vue de la surreprésentation statistique de certains patterns. Un pattern qui apparait significativement plus souvent dans le réseau réel que dans un réseau aléatoire est appelé motif (Milo et al., 2002; Shen-Orr et al., 2002). La figure 8b nous montre que l'on retrouve beaucoup plus souvent des boucles de rétroaction négative et des "feed forward loop" (que je renonce pour l'instant à traduire par "boucle d'action avant") par rapport à un réseau aléatoire. L'idée proposée par l'équipe de Uri Alon (Alon, 2006) c'est que ces motifs surreprésentés ont dû être préservés au cours de l'évolution contre les mutations qui modifient les flèches de manière aléatoire. En effet pour abolir un site de liaison protéine--ADN, il ne suffit en général que d'une seule mutation (1 seul changement de base/lettre ATCG). Or s'ils ont été préservés, c'est qu'ils ont été sélectionnés pour un avantage qu'ils apportent à l'organisme. La topologie du motif, c'est-à-dire sa structure aurait une fonction. La fonction a priori évidente d'une boucle de rétroaction négative (qui agit comme un thermostat), c'est de préserver l'homéostasie de l'organisme. A l'inverse, une boucle de rétroaction positive peut aider, chez les organismes supérieurs, à la différentiation irréversible des cellules dans une voie ou une autre. Mais il existe aussi des fonctions plus subtiles, impossibles à comprendre sans l'utilisation d'un modèle mathématique. C'est ce que nous allons étudier maintenant.

Fonction de quelques motifs courants

La boucle de rétroaction négative

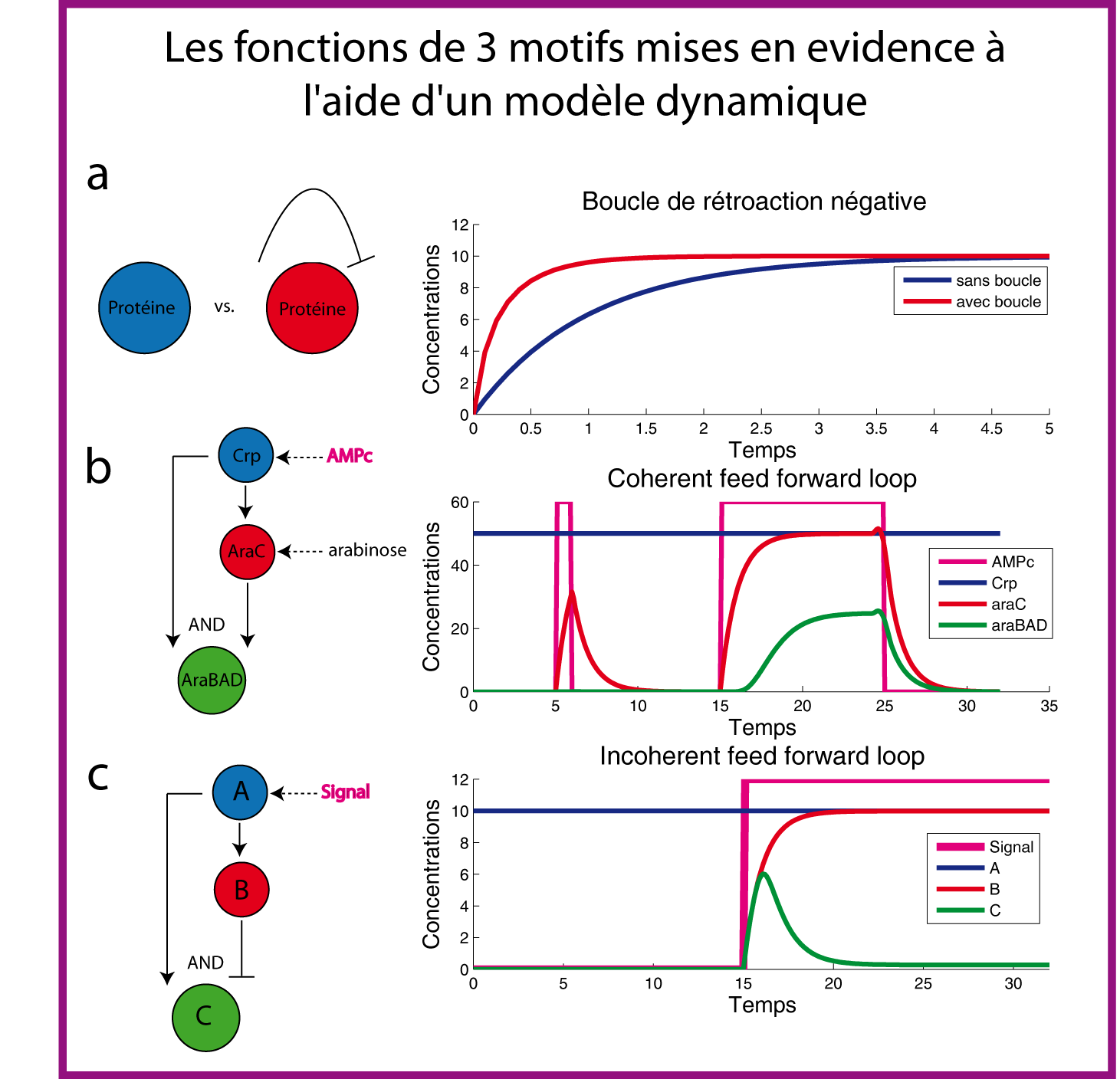
Recherchons une des fonctions de la boucle de rétroaction négative grâce à un petit modèle ODE (figure 9a). On observe que la courbe rouge (avec boucle de rétroaction négative) atteint l'état d'équilibre plus vite que la courbe bleue (sans boucle de rétroaction négative). Cela semble contre-intuitif mais notez bien que pour obtenir ce résultat, le taux de synthèse (force du promoteur) de l'équation avec boucle de rétroaction est choisi 5 fois plus grand que celui de l'équation sans boucle de rétroaction. Vous voyez donc que, pour un même état d'équilibre, la boucle de rétroaction négative accélère la réponse à un signal donné. Cela a également été démontré expérimentalement (Rosenfeld et al., 2002) dans le contexte du système de réparation de l'ADN (SOS) dont j'ai déjà parlé dans le chapitre sur E. coli .

Le "feed forward loop" cohérent (type 1 avec un porte AND)

Ce motif peut agir comme "détecteur de persistance" (Mangan & Alon, 2003). Il a été démontré expérimentalement avec le réseau d'utilisation de l'arabinose (Mangan et al., 2003). Dans ce système, un pulse d'AMPc active la protéine Crp qui active alors l'expression de deux gènes: le gène araC et l'operon araBAD. Ce dernier permet l'utilisation de l'arabinose comme source de carbone. Le gène araC code pour la protéine AraC qui, elle aussi, active, en présence d'arabinose, l'expression de l'operon araBAD. Au final, pour activer araBAD, il faut à la fois Crp et AraC: c'est une porte logique AND. Le "feed forward loop" est dit "cohérent" car la protéine Crp agit (de notre point de vue) de manière cohérente en activant un élément intermédiaire lui aussi chargé d'activer la cible finale. En choisissant judicieusement les paramètres, on peut montrer avec un petit système ODE pourquoi ce réseau peut agir comme détecteur de persistance.

Mais d'abord qu'est ce qu'un détecteur de persistance ? Imaginez une camera dans une gare couplée à un algorithme chargé de détecter automatiquement des objets abandonnés, par exemple, une valise. Dans la gare, des valises posées quelques secondes / minutes à coté de leur propriétaire, il y en a plein. Ce qu'il faut à l'algorithme c'est un filtre qui lui indique les persistances c'est-à-dire les valises qui n'ont pas bougé depuis plus de 5 minutes, par exemple. Cela permet de déclencher une alarme que lorsque cela est vraiment nécessaire. Chez E. coli, c'est la même chose. Des petites variations d'AMPc, des petits pulses, il y en a potentiellement beaucoup. Cela représente du bruit et il ne faut pas activer l'operon araBAD dans ce cas. Ces variations d'activité de Crp sont insuffisantes pour que la concentration d'AraC dépasse un seuil suffisant pour l'activation de l'operon araBAD. Au contraire, ce que la bactérie veut détecter, c'est une concentration d'AMPc qui augmente et se maintient suffisamment longtemps. Quand tel est le cas, la concentration de la protéine AraC finit par dépasser un certain seuil. La présence conjointe de Crp et d'AraC permet à la porte AND de fonctionner et d'activer l'operon araBAD (figure 9b).

Le "feed forward loop" incohérent (type 1 avec un porte AND)

Ce motif peut agir comme un "générateur de pulse" (Mangan & Alon, 2003). Il a été démontré expérimentalement avec un petit système synthétique multicellulaire (Basu et al., 2005). Voyons quelle est la dynamique de ce motif avec le modèle ODE de la figure 9c. Un signal active la protéine A. Celle-ci active l'expression des protéine B et C. Mais quand la protéine B commence à s'accumuler, elle réprime l'expression de C, d'où le pulse observé.

                
function MotifAlon
figure('Color', 'w')
for i=1:3 % genere 3 petit plots et leur attribut un handle
    Handle(i)=subplot(3,1,i);
    hold(Handle(i));
end
% système d'equation de la figure 1
% boucle de retroaction négative
    function dydt = equations1(t,y)
        dydt=zeros(2,1);
        dydt(1) = kappa-gamma*y(1);
        dydt(2) = kappa2*(kd.^n/(kd.^n+y(2).^n))- gamma2*y(2);
    end
% système d'equation de la figure 2
% feed forward loop coherent
    function dydt = equations2(t,y)
        dydt=zeros(3,1);
        AMPc=AMPC*(t>5&&t<6)||(t>15&&t<25);
        dydt(1) = kappa-gamma*y(1);
        dydt(2) = kappa*(y(1).^n*AMPc.^n)/(kd2.^n+AMPc.^n)/...
(kd.^n+(y(1).^n*AMPc.^n)/(kd2.^n+AMPc.^n))- gamma*y(2);
        dydt(3) = kappa*(y(2).^n/(kd3.^n+y(2).^n))*(y(1).^n*AMPc.^n)...
/(kd2.^n+AMPc.^n)/(kd.^n+(y(1).^n*AMPc.^n)/(kd2.^n+AMPc.^n))- gamma*y(3);
    end
% système d'equation de la figure 3
% feed forward loop incoherent
    function dydt = equations3(t,y)
        dydt=zeros(3,1);
        Signal2=Signal*(t>15);
        dydt(1) = kappa-gamma*y(1);
        dydt(2) = kappa*(y(1).^n*Signal2.^n)/(kd2.^n+Signal2.^n)...
/(kd.^n+(y(1).^n*Signal2.^n)/(kd2.^n+Signal2.^n))- gamma*y(2);
        dydt(3) = kappa*(kd3.^n/(kd3.^n+y(2).^n))*(y(1).^n*Signal2.^n)...
/(kd2.^n+Signal2.^n)/(kd.^n+(y(1).^n*Signal2.^n)/(kd2.^n+Signal2.^n))...
- gamma*y(3);
    end
% 3 boucles pour simuler les 3 systemes et plotter les données
% correspondantes
for i=1:3
    if i==1   % boucle de retroaction négative
        n=2;kappa=10;kappa2=50;kd=5; gamma=1; gamma2=1;
        % vous remarquez que kappa2 est 5 fois plus fort que kappa1
        yo=[0 0];%condition initiale
        Options = odeset('NonNegative',[1,2]);
        Time=[0:0.1:5];
        [t,y]=ode45(@equations1,Time,yo, Options);%integration
        plot(Handle(1),t, y(:,1),'-b','LineWidth',3)
        plot(Handle(1),t, y(:,2),'-r','LineWidth',3)
        xlabel(Handle(1),'Temps','FontSize',14)
        ylabel(Handle(1),'Concentrations','FontSize',14)
        title(Handle(1),'Boucle de retro-action négative','FontSize',16)
        legend(Handle(1),'sans boucle','avec boucle');
        axis(Handle(1),[0 5 0 12])
    end
    if i==2 % feed forward loop coherent
        n=10;kappa=50;kd=5;kd2=5;kd3=50;gamma=1;gamma2=1;AMPC=60;
        yo=[50 0 0];%condition initiale
        Options = odeset('NonNegative',[1,2,3]);
        Time=[0:0.1:32];
        [t,y]=ode45(@equations2,Time,yo, Options);%integration
        plot(Handle(2),t, AMPC*((t>5&t<6)|(t>15&t<25)),'-m','LineWidth',3)
        plot(Handle(2),t, y(:,1),'-b','LineWidth',3)
        plot(Handle(2),t, y(:,2),'-r','LineWidth',3)
        plot(Handle(2),t, y(:,3),'-g','LineWidth',3)
        xlabel(Handle(2),'Temps','FontSize',14)
        ylabel(Handle(2),'Concentrations','FontSize',14)
        title(Handle(2),'Coherent feed forward loop','FontSize',16)
        legend(Handle(2),'AMPc','Crp','araC','araBAD');
    end
    if i==3% feed forward loop incoherent        
        n=10; kappa=10;kd=5;kd2=5;kd3=7;gamma=1;gamma2=1;Signal=12;
        yo=[10 0 0];%condition initiale
        Options = odeset('NonNegative',[1,2,3]);
        Time=[0:0.1:32];
        [t,y]=ode45(@equations3,Time,yo, Options);%integration
        plot(Handle(3),t, Signal*(t>15),'-m','LineWidth',5)
        plot(Handle(3),t, y(:,1),'-b','LineWidth',3)
        plot(Handle(3),t, y(:,2),'-r','LineWidth',3)
        plot(Handle(3),t, y(:,3),'-g','LineWidth',3)
        xlabel(Handle(3),'Temps','FontSize',14)
        ylabel(Handle(3),'Concentrations','FontSize',14)
        title(Handle(3),'Incoherent feed forward loop','FontSize',16)
        legend(Handle(3),'Signal','A','B','C');
        axis(Handle(3),[0 32 0 12])
    end
end
end
                
            

Les critiques

3 critiques s'opposent à l'idée que la topologie (la structure) d'un réseau (d'un motif) détermine la fonction par le biais de la sélection (évolution):

• Comme nous l'avons vu, à une topologie ne correspond pas nécessairement une seule fonction. Les valeurs numériques des paramètres comptent et en les faisant varier, on peut passer par plusieurs régimes dynamiques possibles (Voigt et al., 2005).
• Le motif est toujours étudié de manière isolée or les connexions du motif au reste du réseau sont trop importantes/influentes pour que l'on puisse inférer sa fonction à partir de la seule structure locale (Knabe et al., 2008).
• Le fait que certains motifs soient statistiquement plus nombreux dans un réseau biologique réel par rapport à un réseau aléatoire n'est pas dû à la sélection du motif pour sa fonction mais plutôt à la topologie "invariante d'échelle" du réseau biologique réel. Comme nous l'avons vu, cette topologie crée des "hubs" et ces derniers favorisent l'apparition de "feed forward loop" par rapport à un réseau strictement aléatoire (Konagurthu & Lesk, 2008).

Etudier la dynamique de réseaux plus gros

Nous avons, pour l'instant, étudié la dynamique de petits motifs réels trouvés chez E. coli ou des petits réseaux synthétique crées par l'homme. Mais ces réseaux n'ont jamais dépassé 3 gènes. Or le génome d'E. coli compte 4000 gènes. Peut-on passer à l'étape suivante et simuler la dynamique de fonctionnement de réseaux plus gros contenant 5, 10, 25, 200 puis 4000 gènes ?

Si on met de coté les erreurs dues à l'utilisation de méthodes numériques, le formalisme ODE étudié dans ce chapitre n'a pas de limites intrinsèques et pourrait donc, en théorie, simuler un réseau de 4000 gènes sans difficulté. Pour un réseau très linéaire sans boucle de rétroaction, on peut augmenter le nombre de gènes sans trop diminuer la qualité des prédictions effectuées. Mais dés lors que le système devient non linéaire (boucles de rétroaction) ou que la connectivité (nombre de liens par noeud) augmente trop, les prédictions deviennent fortement dépendantes des conditions initiales et de la valeur numérique des paramètres. C'est ce qu'on appelle la dépendance sensitive aux conditions initiales (le populaire effet papillon). Pour proposer un exemple simple, une toute petite différence dans la valeur d'un paramètre (15,000007 par rapport à 15,000008) aura des conséquences énormes sur le phénotype final: la cellule vit ou la cellule meurt. Pour couronner le tout, dites vous que ce problème existe dans un système déterministe et il est évidemment amplifié dans un système stochastique (c'est le cas de la cellule) ce qui accroit encore les incertitudes sur le phénotype final. Or malgré son réseau non linéaire au fonctionnement stochastique, la cellule réussit à se prémunir de cette dépendance sensitive aux conditions initiales de manière évidente. En effet, lors de son adaptation à divers stimuli, la population de cellules, via son réseau de régulation, semble réussir à basculer vers le phénotype adéquate en calculant la solution optimale et ce de manière reproductible et donc un minimum déterministe. Comment fait-elle ?

En électronique, un module est défini comme une unité fonctionnelle qui est capable de maintenir ses propriétés intrinsèques indépendamment de ses connections externes. C'est un concept important car il permet aux ingénieurs de connecter plusieurs éléments ensembles sur une puce tout en maintenant la capacité de prédire le comportement de l'ensemble (le résultat après assemblage). Beaucoup de biologistes pensent que pour être suffisamment robuste, le réseau d'un organisme vivant doit être composé de modules c'est-à-dire être modulaire (Hartwell et al., 1999; Wolf & Arkin, 2003; Kashtan & Alon, 2005). Selon Gunter Wagner, la question n'est même plus tant de savoir si les réseaux sont modulaires, mais plutôt quelle est l'origine de cette modularité (sélection naturelle ?) et quelles sont ses conséquences sur "l' évolvabilité" d'un organisme (Wagner et al., 2007).

Un des enjeux futurs de la biologie synthétique sera de construire ces réseaux modulaires dont on contrôle le comportement d'ensemble. Pour cela, il faudra assembler des petits modules et utiliser le savoir faire de l'électronique pour minimiser les phénomènes de rétroactivité (Del Vecchio et al., 2008; Sauro, 2008). Réussir à connecter ensembles quelques petits modules de 2 à 4 gènes et démontrer qu'on contrôle le fonctionnement global sera déjà une belle avancée. Pour cela, il faut selon moi, limiter la taille des modèles dynamiques (moins de 10--15 gènes). En effet, ces derniers doivent rester prédictifs de manière à permettre à l'expérimentateur d'utiliser ces prédictions pour ajuster les paramètres via les techniques de biologies moléculaires.

Il me semble que les novices ont tendance à sous-estimer la difficulté technique que représente le contrôle quantitatif d'une seule interaction. Le passage du contrôle d'un réseau de n interactions à n+1 peut prendre énormément de temps (mois, années). Le repressilator que nous avons étudié contient 3 gènes et 3 interactions et c'est un exploit technique qui prendrait des années à être reproduit par une équipe d'aujourd'hui.

En biologie synthétique, je pense qu'il faut privilégier les petits modèles (simples mais pas simplistes). Les gros modèles contenant des dizaines/centaines de gènes et métabolites sont beaucoup trop gros pour être réellement prédictifs au sens où je l'entends. Ces modèles ne peuvent pas me fournir une prédiction fiable m'indiquant comment modifier certains paramètres de mon réseau pour adapter son comportement dynamique. Or la sureté des prédictions est primordiale car la modification de la séquence ADN pour ajuster un paramètre (biologie moléculaire) est très fastidieuse et peut prendre des mois. Pourtant et paradoxalement, les prédictions générées par ces gros modèles sont souvent justes. La raison est simple : le chercheur connaît son but et finit donc évidemment par l'atteindre. Comme le souligne Antoine Danchin, beaucoup de modèles redécouvrent le cycle de Krebs.

Pour faire de la biologie synthétique bottum-up, il faut vérifier et contrôler expérimentalement chaque interaction. Cela peut prendre du temps et se fait parfois dans la douleur mais c'est indispensable. Les interactions données sur les bases de données comme Ecocyc ou RegulonDB devraient être considérées comme fausses a priori jusqu'à confirmation expérimentale. Comprenez-moi bien, ce n'est pas une critique envers ces bases de données, ni envers le travail des chercheurs qui ont découverts ces interactions. C'est le constat qu'on se trouve ici à la frontière de la connaissance et cette connaissance reste relative et n'attend qu'à être améliorée. En biologie, ce qui est vrai dans un laboratoire sera faux dans celui d'à coté. Parfois, un chercheur qui décrit/propose une nouvelle interaction va, lui-même, ajouter du conditionnel dans sa publication initiale. Puis au fil des années et des publications citant cette interaction, le conditionnel disparait et petit à petit l'interaction devient sacrée. Pourquoi, dans les bases de données, n'y a t'il pas de chiffres, même indicatifs, associés à une interaction ? Par exemple, dans tel condition, ce facteur de transcription active d'un facteur 100 l'expression de ce gène ou au contraire, il ne l'active que de 2%. Il n'y a pas de chiffres car la résolution actuelle de nos expériences ne nous permet pas d'atteindre un tel niveau de standardisation. On est très loin de l'électronique.

Je donne un petit peu mes recettes de cuisine (qui n'engagent que moi) car il me semble que les novices ont parfois tendance à surestimer les informations de topologie. En biologie synthétique, ne faites pas confiance à une information a priori. Vérifiez là toujours par vous-même et rappelez vous que ce qui est facile en théorie est toujours difficile en pratique et ce qui est difficile en théorie est quasiment impossible en pratique.

Bibliographie

1. Alon, U. (2006). "An introduction to system biology."
2. Barabasi, A. and E. Bonaneau (2010). "les reseaux invariants d'echelle." Pour la science.
3. Basu, S., Y. Gerchman, et al. (2005). "A synthetic multicellular system for programmed pattern formation." Nature 434(7037): 1130-4.
4. Chang, D. E., S. Leung, et al. (2009). "Building biological memory by linking positive feedback loops." Proc Natl Acad Sci U S A.
5. Cherry, J. L. and F. R. Adler (2000). "How to make a biological switch." J Theor Biol 203(2): 117-33.
6. Cohn, M. and K. Horibata (1959). "Inhibition by glucose of the induced synthesis of the beta-galactoside-enzyme system of Escherichia coli. Analysis of maintenance." J Bacteriol 78: 601-12.
7. Del Vecchio, D., A. J. Ninfa, et al. (2008). "Modular cell biology: retroactivity and insulation." Mol Syst Biol 4: 161.
8. Elowitz, M. B. and S. Leibler (2000). "A synthetic oscillatory network of transcriptional regulators." Nature 403(6767): 335-8.
9. Gardner, T. S., C. R. Cantor, et al. (2000). "Construction of a genetic toggle switch in Escherichia coli." Nature 403(6767): 339-42.
10. Hartwell, L. H., J. J. Hopfield, et al. (1999). "From molecular to modular cell biology." Nature 402(6761 Suppl): C47-52.
11. Jeong, H., S. P. Mason, et al. (2001). "Lethality and centrality in protein networks." Nature 411(6833): 41-2.
12. Jeong, H., B. Tombor, et al. (2000). "The large-scale organization of metabolic networks." Nature 407(6804): 651-4.
13. Kashtan, N. and U. Alon (2005). "Spontaneous evolution of modularity and network motifs." Proc Natl Acad Sci U S A 102(39): 13773-8.
14. Knabe, J. F., C. L. Nehaniv, et al. (2008). "Do motifs reflect evolved function?--No convergent evolution of genetic regulatory network subgraph topologies." Biosystems 94(1-2): 68-74.
15. Konagurthu, A. S. and A. M. Lesk (2008). "On the origin of distribution patterns of motifs in biological networks." BMC Syst Biol 2: 73.
16. Kondo, T., C. A. Strayer, et al. (1993). "Circadian rhythms in prokaryotes: luciferase as a reporter of circadian gene expression in cyanobacteria." Proc Natl Acad Sci U S A 90(12): 5672-6.
17. Lima-Mendez, G. and J. van Helden (2009). "The powerful law of the power law and other myths in network biology." Mol Biosyst 5(12): 1482-93.
18. Mangan, S. and U. Alon (2003). "Structure and function of the feed-forward loop network motif." Proc Natl Acad Sci U S A 100(21): 11980-5.
19. Mangan, S., A. Zaslaver, et al. (2003). "The coherent feedforward loop serves as a sign-sensitive delay element in transcription networks." J Mol Biol 334(2): 197-204.
20. Mihalcescu, I., W. Hsing, et al. (2004). "Resilient circadian oscillator revealed in individual cyanobacteria." Nature 430(6995): 81-5.
21. Milo, R., S. Shen-Orr, et al. (2002). "Network motifs: simple building blocks of complex networks." Science 298(5594): 824-7.
22. Novick, A. and M. Weiner (1957). "Enzyme Induction as an All-or-None Phenomenon." Proc Natl Acad Sci U S A 43(7): 553-66.
23. Ozbudak, E. M., M. Thattai, et al. (2004). "Multistability in the lactose utilization network of Escherichia coli." Nature 427(6976): 737-40.
24. Ravasz, E., A. L. Somera, et al. (2002). "Hierarchical organization of modularity in metabolic networks." Science 297(5586): 1551-5.
25. Robert, L., G. Paul, et al. "Pre-dispositions and epigenetic inheritance in the Escherichia coli lactose operon bistable switch." Mol Syst Biol 6: 357.
26. Rosenfeld, N., M. B. Elowitz, et al. (2002). "Negative autoregulation speeds the response times of transcription networks." J Mol Biol 323(5): 785-93.
27. Sauro, H. M. (2008). "Modularity defined." Mol Syst Biol 4: 166.
28. Shen-Orr, S. S., R. Milo, et al. (2002). "Network motifs in the transcriptional regulation network of Escherichia coli." Nat Genet 31(1): 64-8.
29. Stricker, J., S. Cookson, et al. (2008). "A fast, robust and tunable synthetic gene oscillator." Nature 456(7221): 516-9.
30. Voigt, C. A., D. M. Wolf, et al. (2005). "The Bacillus subtilis sin operon: an evolvable network motif." Genetics 169(3): 1187-202.
31. Wagner, G. P., M. Pavlicev, et al. (2007). "The road to modularity." Nat Rev Genet 8(12): 921-31.
32. Wolf, D. M. and A. P. Arkin (2003). "Motifs, modules and games in bacteria." Curr Opin Microbiol 6(2): 125-34.

Notes de bas de page

1. Michel Morange, La vie expliquée, Odile Jacob p. 158.